如图甲所示，水平面上固定两条足够长的平行轨道，轨道间距为$0.4\;\rm m$，虚线${{O}_{1}}{{O}_{2}}$垂直于轨道，${{O}_{1}}{{O}_{2}}$左侧部分轨道由金属材料制成，其左端通过导线与电容为$2\times {{10}^{3}}\;\rm \mu\!\!{ F}$的平行板电容器的极板$A$、$B$分别相连，${{O}_{1}}{{O}_{2}}$右侧部分的轨道由绝缘材料制成，轨道处于方向竖直向下的匀强磁场中。将一质量为$0.1\;\rm kg$且电阻不计的金属棒$MN$置于${{O}_{1}}{{O}_{2}}$左侧的金属轨道上，并通过水平轻绳绕过光滑定滑轮与质量为$0.2\;\rm kg$的小物块相连，$MN$与轨道各部分的动摩擦因数都相同。$t=0$时刻，将$MN$和小物块同时由静止释放，$MN$离开虚线${{O}_{1}}{{O}_{2}}$后的图像如图乙所示。整个过程中$MN$始终垂直于轨道且与轨道接触良好，电容器未被击穿，重力加速度$g=10\;\rm \text{m}/{{\text{s}}^{2}}$。则下列说法正确的是$(\qquad)$

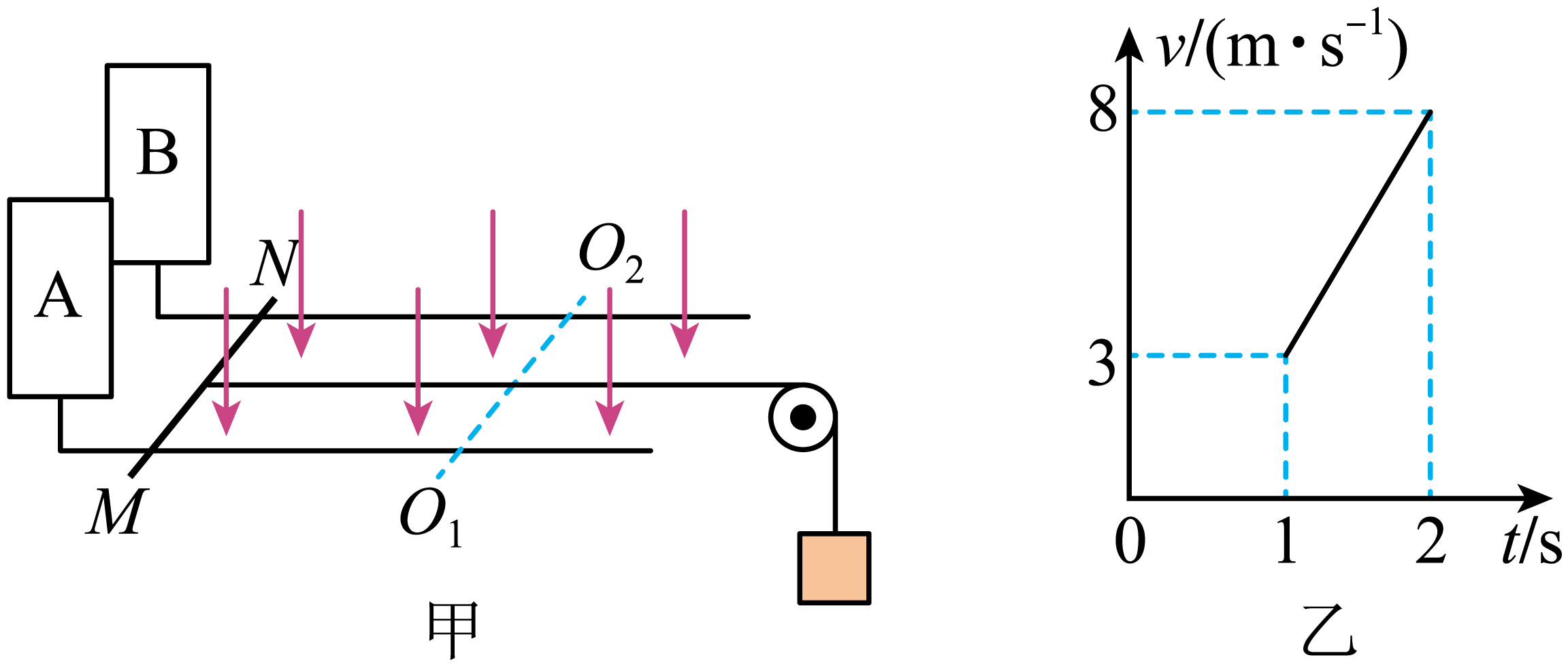
电容器的$A$极板带正电

$MN$在第$1\\;\\rm s$内做匀加速直线运动

磁场的磁感应强度大小为$25\\;\\rm T$

电容器储存的电能为$0.9\\;\\rm J$

$\rm A$．金属棒切割磁感线时，根据右手定则可知电流方向由$M$流向$N$，则电容器的$B$极板带正电，故$\rm A$错误；

$\rm B$．设金属棒的质量为$m$，则小物块质量为$M$，轨道间距为$d$，金属棒在虚线${{O}_{1}}{{O}_{2}}$左侧运动时，以小物块和金属棒为整体，根据牛顿第二定律可得$Mg-BId-\mu mg=(M+m)a$

又$I=\dfrac{\Delta q}{\Delta t}=\dfrac{C\Delta U}{\Delta t}=\dfrac{CBd\Delta v}{\Delta t}=CBda$

联立可得$a=\dfrac{Mg-\mu mg}{C{{B}^{2}}{{d}^{2}}+M+m}$

可知金属棒在虚线${{O}_{1}}{{O}_{2}}$左侧做初速度为零的匀加速直线运动，故$\rm B$正确；

$\rm C$．根据$v-t$图像可知，金属棒在虚线${{O}_{1}}{{O}_{2}}$左侧运动时间为$1\;\rm s$，末速度为$3\;\rm m/s$，则加速度为$a=\dfrac{\Delta v}{\Delta t}=3{\;\rm m/s}^{2}$

且$a=\dfrac{Mg-\mu mg}{C{{B}^{2}}{{d}^{2}}+M+m}$

$1\sim2\;\rm \text{s}$内金属棒在虚线${{O}_{1}}{{O}_{2}}$右侧运动，以金属棒和小滑块为整体，根据牛顿第二定律可得$Mg-\mu mg=(M+m){a}'$

根据$v-t$图像可知，$1\sim2\text{s}$内金属棒在虚线${{O}_{1}}{{O}_{2}}$右侧运动的加速度为${a}'=\dfrac{\Delta {v}'}{\Delta {t}'}=\dfrac{8-3}{2-1}\;\rm m/s^2=5\;\rm m/s^2$

联立解得$\mu =0.5$，$B=25\;\rm {T}$，故$\rm C$正确；

$\rm D$．金属棒的释放点到虚线${{O}_{1}}{{O}_{2}}$的距离为$x=\dfrac{1}{2}at_{1}^{2}=\dfrac{1}{2}\times 3\times {{1}^{2}}\;\rm \text{m}=1.5\;\rm \text{m}$

$1\;\rm \text{s}$末金属棒的速度为$3\;\rm \text{m/s}$，根据功能关系可知$Mgx-\mu mgx=E+\dfrac{1}{2}\times (M+m){{v}_{1}}^{2}$

解得电容器储存的电能为$E=0.9\;\rm \text{J}$，故$\rm D$正确。

故选：$\rm BCD$。