如图，两条固定的光滑平行金属导轨，所在平面与水平面夹角为$\theta$，间距为$l$，导轨电阻忽略不计，两端各接一个阻值为$2R$的定值电阻，形成闭合回路：质量为$m$的金属棒垂直导轨放置，并与导轨接触良好，接入导轨之间的电阻为$R$；劲度系数为$k$的两个完全相同的绝缘轻质弹簧与导轨平行，一端固定，另一端均与金属棒中间位置相连，弹簧的弹性势能$E_{p}$与形变量$x$的关系为$E_{p}=\dfrac{1}{2}kx^{2}$；将金属棒移至导轨中间位置时，两弹簧刚好处于原长状态；整个装置处于垂直导轨所在平面向上的匀强磁场中，磁感应强度大小为$B$。将金属棒从导轨中间位置向上移动距离$a$后静止释放，金属棒沿导轨向下运动到最远处，用时为$t$，最远处与导轨中间位置距离为$b$，弹簧形变始终在弹性限度内。此过程中$(\qquad)$

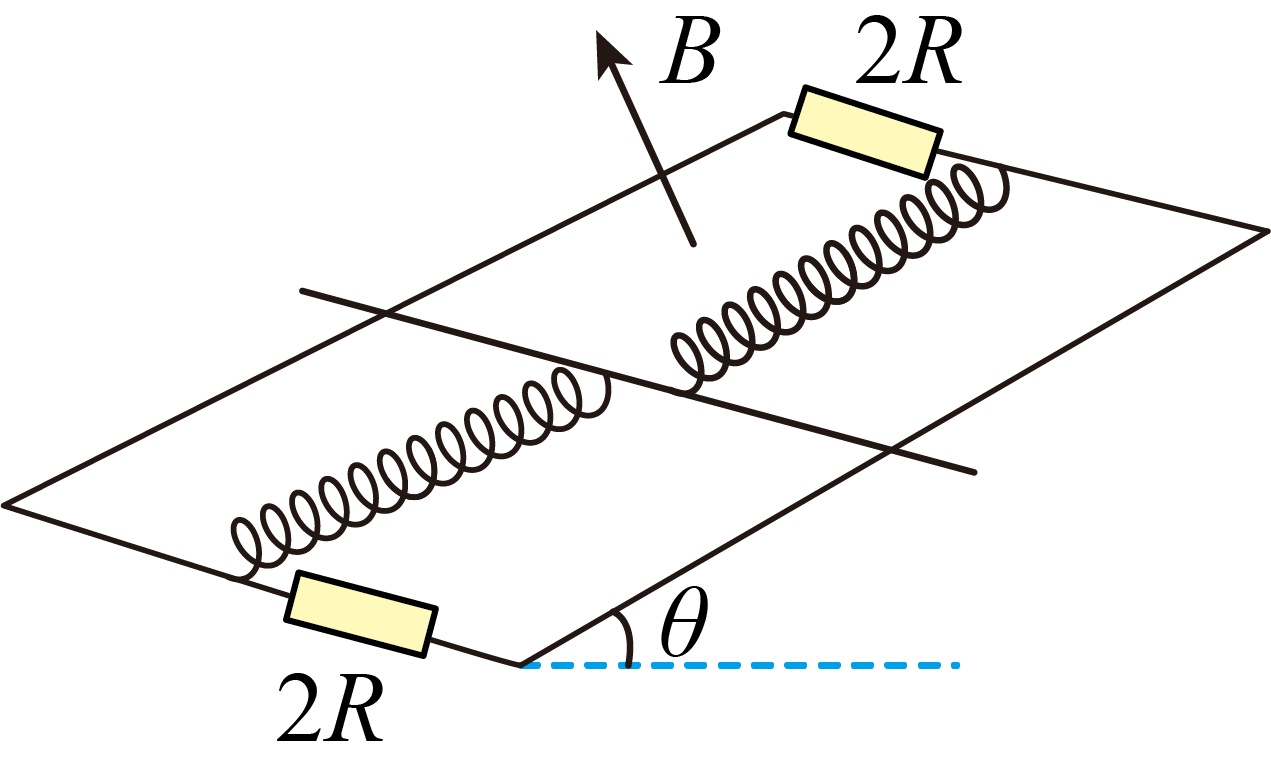
金属棒所受安培力冲量大小为$\\dfrac{B^{2}l^{2}(a+b)}{R}$

每个弹簧对金属棒施加的冲量大小为$\\dfrac{B^{2}l^{2}(a+b)}{4R}+\\dfrac{mgt\\sin\\theta}{2}$

每个定值电阻产生的热量为$\\dfrac{k\\left( a^{2}-b^{2} \\right)}{8}+\\dfrac{mg(a+b)\\sin\\theta}{4}$

金属棒的平均输出功率为$\\dfrac{k\\left( a^{2}-b^{2} \\right)+mg(a+b)\\sin\\theta}{2t}$

$\rm A$．根据$I_{安}=B\overline{I}l\Delta t=Blq$

而$q=\dfrac{\overline{E}}{R_{总}}\Delta t=\dfrac{\Delta\Phi}{R_{总}}=\dfrac{Bl(a+b)}{R_{总}}$，$R_{总}=\dfrac{2R \cdot 2R}{2E+2R}+R=2R$

解得$I_{安}=\dfrac{B^{2}l^{2}(a+b)}{2R}$，选项$\rm A$错误；

$\rm B$．该过程中由动量定理$2I_{弹}-I_{安}+mg\sin \theta ⋅ t=0$

解得每个弹簧对金属棒施加的冲量大小为$I_{弹}=\dfrac{1}{2}I_{安}-\dfrac{1}{2}mgt\sin\theta=\dfrac{B^{2}l^{2}(a+b)}{4R}-\dfrac{1}{2}mgt\sin\theta$，选项$\rm B$错误；

$\rm C$．由能量关系可知回路产生的总热量$Q=mg\sin\theta(a+b)+2 \times \dfrac{1}{2}ka^{2}-2 \times \dfrac{1}{2}kb^{2}$

每个定值电阻产生的热量为$Q_{1}=\dfrac{1}{4}Q=\dfrac{mg\sin\theta(a+b)}{4}+\dfrac{1}{4}k(a^{2}-b^{2})$，选项$\rm C$错误；

$\rm D$．金属棒的平均输出功率$\overline{P}=\dfrac{\dfrac{1}{2}Q}{t}=\dfrac{mg\sin\theta(a+b)+k(a^{2}-b^{2})}{2t}$，选项$\rm D$正确。

故选：$\rm D$。