高中 | 能量守恒定律 题目答案及解析
稿件来源:高途
高中 | 能量守恒定律题目答案及解析如下,仅供参考!
选修3-3
第十章 热力学定律
10.3 热力学第一定律 能量守恒定律
能量守恒定律
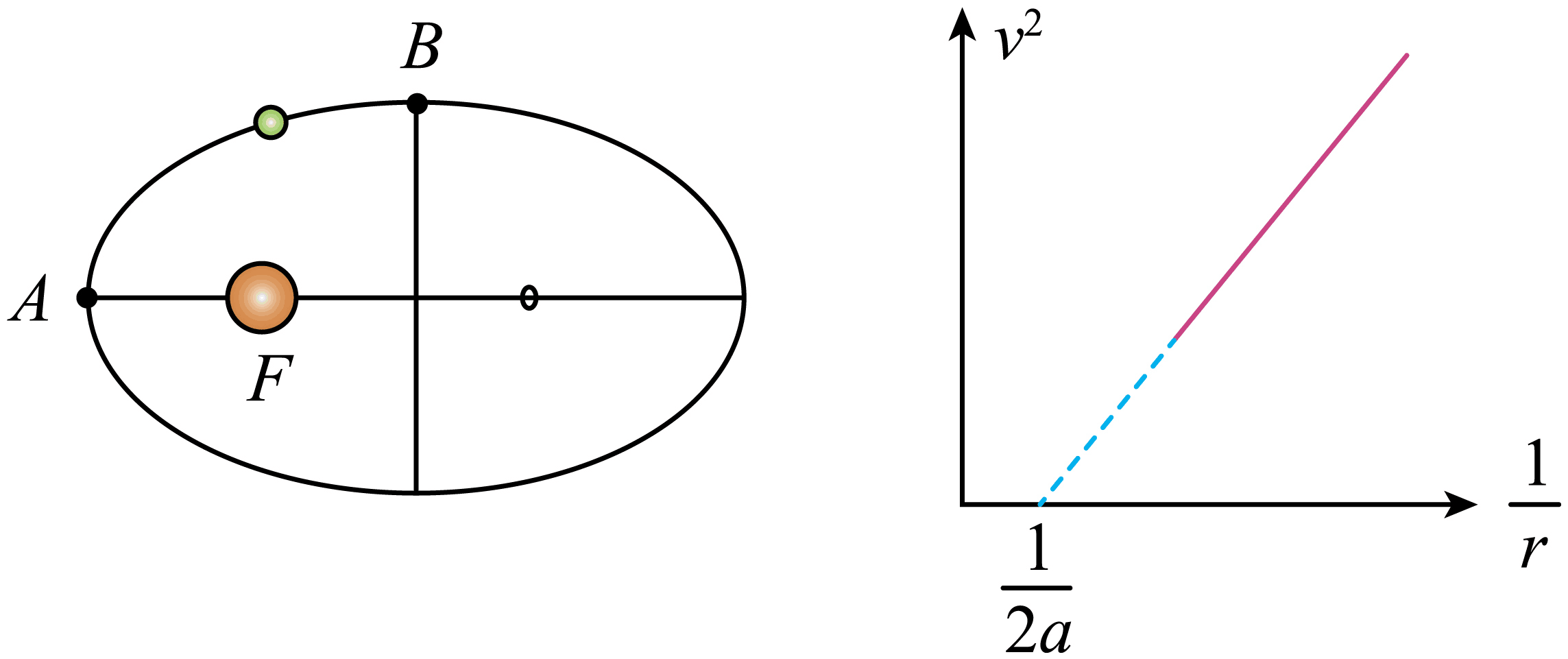
带电粒子绕着带电量为$+Q$的源电荷做轨迹为椭圆的曲线运动,源电荷固定在椭圆左焦点$F$上,带电粒子电量为$−q$;已知椭圆焦距为$c$,半长轴为$a$,电势计算公式为$\varphi=\dfrac{kQ}{r}$,带电粒子速度的平方与其到电荷的距离的倒数满足如图关系。
求在椭圆轨道半短轴顶点$B$的电势;
$\\varphi_{B}= \\dfrac{kQ}{a}$
"]]由几何关系可知,椭圆上任何一点到两焦点间距离之和为$2a$,故顶点$B$距源电荷的距离为$r=a$
根据电势计算公式$\varphi=\dfrac{kQ}{r}$可得在椭圆轨道半短轴顶点$B$的电势为$\varphi_{B}=\dfrac{kQ}{a}$
求带电粒子从$A$到$B$的运动过程中,电场力对带电粒子做的功;
$- kQq\\left(\\dfrac{2}{2a-c}- \\dfrac{1}{a}\\right)$
"]]同理可知,在椭圆轨道半长轴顶点$A$的电势为$\varphi_{A}=\dfrac{kQ}{a-\dfrac{c}{2}}= \dfrac{2kQ}{2a-c}$
根据电场力做功与电势能的关系可知,带电粒子从$A$到$B$的运动过程中,电场力对带电粒子做的功为$W_{AB}=- q(\varphi_{A}-\varphi_{B})=- kQq\left(\dfrac{2}{2a-c}-\dfrac{1}{a}\right)$
用推理论证带电粒子动能与电势能之和是否守恒;若守恒,求其动能与电势能之和;若不守恒,说明理由。
守恒,$- \\dfrac{kQq}{2a}$
"]]设带电粒子的质量为$m$,假设带电粒子动能与电势能之和守恒,则满足$\dfrac{1}{2}mv^{2}+(-q)\dfrac{kQ}{r}= C$(定值)
则$v^{2}=\dfrac{2kQq}{m} \cdot \dfrac{1}{r}+\dfrac{2C}{m}$
根据图像可知$v^{2}-\dfrac{1}{r}$关系为一条倾斜直线,故假设成立,将图像中$\left(\dfrac{1}{2a},0\right)$代入关系式可得其动能与电势能之和为$C=- \dfrac{kQq}{2a}$
高中 | 能量守恒定律题目答案及解析(完整版)
