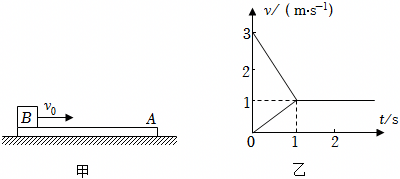
如图所示，长木板$A$放在光滑的水平面上，质量为$m=2\;\rm kg$的另一物体$B$以水平速度$v_{0}=3\;\rm m/s$滑上原来静止的长木板$A$的表面，由于$A$、$B$间存在摩擦，之后$A$、$B$速度随时间变化情况如图乙所示，则下列说法正确的是$(\qquad)$

木板获得的动能为$2\\;\\rm J$

系统损失的机械能为$4\\;\\rm J$

木板$A$的最小长度为$1.5\\;\\rm m$

$A$、$B$间的动摩擦因数为$0.1$

$\rm A$、由图示图像可知，木板获得的速度为 $v=1\;\rm m/s$，$A$、$B$组成的系统动量守恒，以$B$的初速度方向为正方向，根据动量守恒定律可得：

$mv_{0}=(m+m_{A})v$

得：$m_{A}=4$ $kg$，则$A$的动能为 $E_{k}= \dfrac{1}{2}m_{A}v^{2}= \dfrac{1}{2} \times4\times 1^{2}=2\;\rm J$，故$\rm A$正确。

$\rm B$、系统损失的动能$\Delta E_{k}= \dfrac{1}{2}mv^{2}- \dfrac{1}{2}(m_{A}+m)v^{2}= \dfrac{1}{2} \times2\times 3^{2}- \dfrac{1}{2} \times6\times 1^{2}=6\;\rm J$，故$\rm B$错误。

$\rm C$、木板$A$的长度 $L\geqslant \dfrac{1}{2}v_{0}t_{1}= \dfrac{3 \times 1}{2}\;\rm m=1.5\;\rm m$，最小长度为$1.5\;\rm m$，故$\rm C$正确。

$\rm D$、$B$的加速度大小：$a= \dfrac{\Delta v}{\Delta t}=\dfrac{3-1}{1} =2\;\rm m/s^{2}$，由牛顿第二定律得 $\mu mg=ma$，得 $\mu =0.2$，故$\rm D$错误。

故选：$\rm AC$。