高中 | 动能定理的理解与一般应用 题目答案及解析
稿件来源:高途
高中 | 动能定理的理解与一般应用题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.7 动能和动能定理
动能定理的理解与一般应用
医院中$X$光检测设备的核心器件为$X$射线管。如图所示,在$X$射线管中,电子(质量为$m$、电荷量为$-e$,初速度可以忽略)经电压为$U$的电场加速后,从$P$点垂直磁场边界水平射入匀强磁场中。磁场宽为$2L$,磁感应强度大小可以调节。电子经过磁场偏转后撞击目标靶,撞在不同位置就会辐射出不同能量的$X$射线。已知水平放置的目标靶$MN$长为$2L$,$PM$长为$L$,不计电子重力、电子间相互作用力及电子高速运行中辐射的能量。
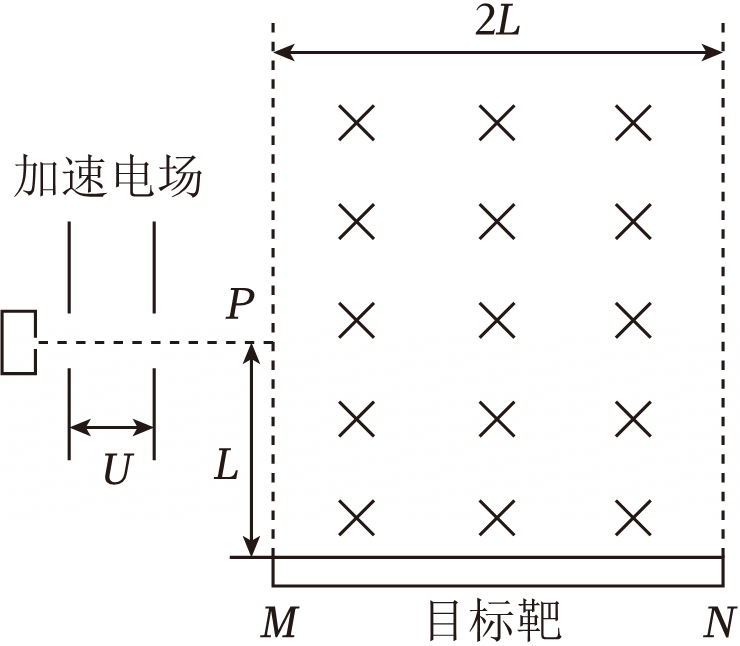
求电子进入磁场的速度大小;
求电子进入磁场的速度大小为$\\sqrt{\\dfrac{2eU}{m}}$
"]]在加速电场中,根据动能定理有$eU=\dfrac{1}{2}mv^{2}$,解得 $v=\sqrt{\dfrac{2eU}{m}}$
调节磁感应强度大小使电子垂直撞击在目标靶上,求电子在磁场中运动的时间;
调节磁感应强度大小使电子垂直撞击在目标靶上,求电子在磁场中运动的时间为$\\dfrac{\\pi L}{4}\\sqrt{\\dfrac{2m}{eU}}$
"]]设电子垂直打在$MN$中间时,做匀速圆周运动的半径为 $R_{1}$,由几何关系得 $R_{1}=L$,对应的圆心角为 $\dfrac{\pi}{2}$,又因为$t=\dfrac{\pi R_{1}}{2v}$,联立以上各式解得$t=\dfrac{\pi L}{4}\sqrt{\dfrac{2m}{eU}}$
为使辐射出的$X$射线能量范围最大,求磁感应强度的大小范围。
为使辐射出的$X$射线能量范围最大,磁感应强度的大小范围是$\\dfrac{2\\sqrt{2meU}}{5eL} \\leqslant B \\leqslant \\dfrac{2\\sqrt{2meU}}{eL}$
"]]电子在磁场中运动有$evB=m\dfrac{v^{2}}{R}$,解得 $R=\dfrac{mv}{eB}$,设打在$M$点时的运动半径为 $R_{2}$,依几何关系可知$R_{2}=\dfrac{1}{2}L$,联立以上各式解得磁感应强度最大值为$B_{1}=\dfrac{2\sqrt{2meU}}{eL}$,同理,打在$N$点的半径为 $R_{3}$,依几何关系可知$R_{3}^{2}=(R_{3}-L)^{2}+(2L)^{2}$,联立以上各式解得磁感应强度最小值为$B_{2}=\dfrac{2\sqrt{2meU}}{5eL}$,综上所述,磁感应强度的取值范围为$\dfrac{2\sqrt{2meU}}{5eL} \leqslant B \leqslant \dfrac{2\sqrt{2meU}}{eL}$
高中 | 动能定理的理解与一般应用题目答案及解析(完整版)
