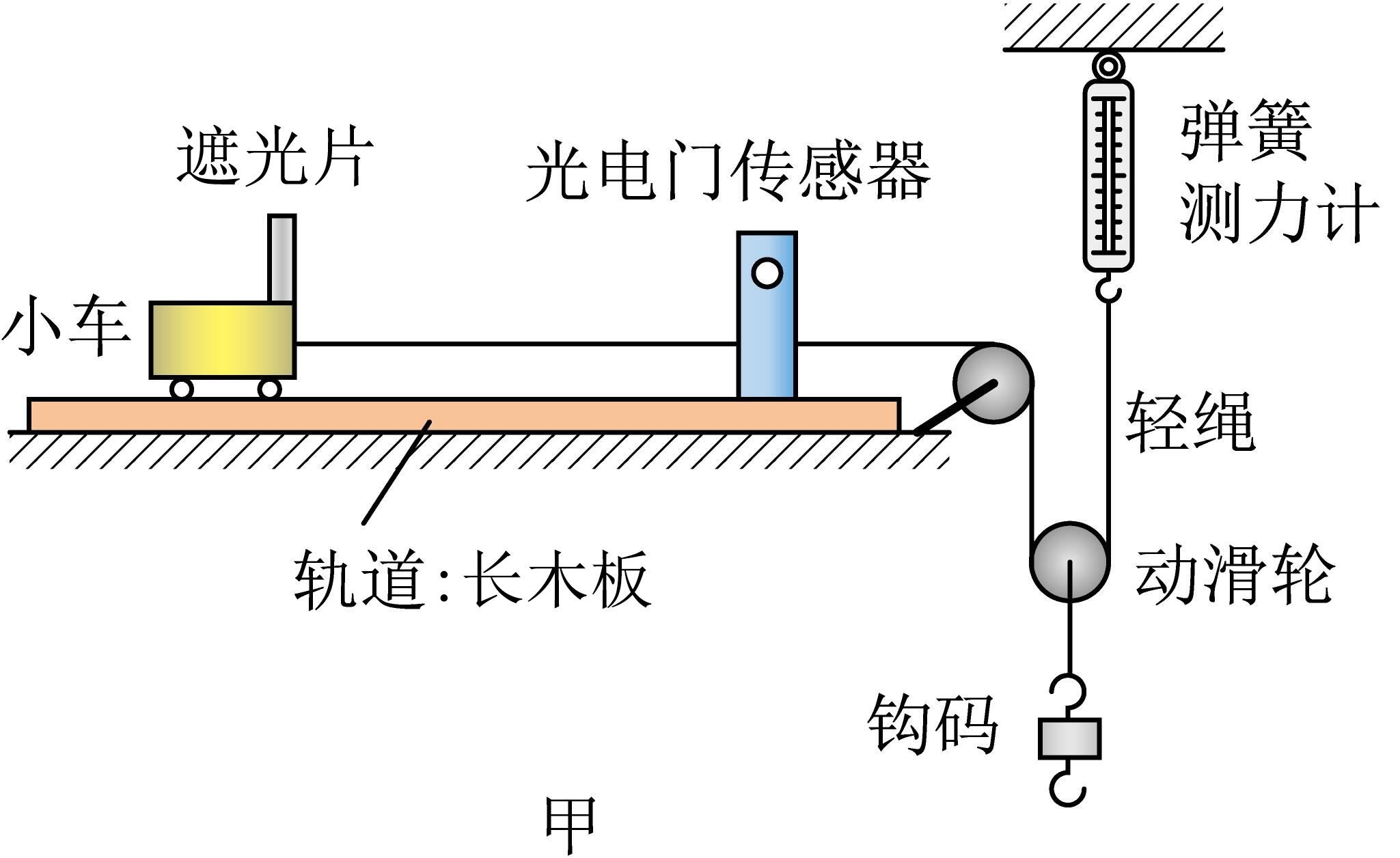
某同学在研究小车加速度与拉力关系的实验中，把小车所受拉力当作合力，下列说法正确的是$(\qquad)$

需要平衡摩擦力

不需要平衡摩擦力

要求钩码的质量远小于小车质量

不要求钩码的质量远小于小车质量

把小车所受拉力当作合力，需要平衡摩擦力，可以根据弹簧测力计直接读出力的大小，不要求钩码的质量远小于小车质量。

故选：$\rm AD$。

在实验操作完全正确的情况下，小明研究组将小车从某一位置由静止释放，测出遮光片的宽度$d$和它通过光电门的挡光时间$\Delta t$，小车静止时的位置到光电门的位移$s$，小车的质量$m$，弹簧测力计的示数$F$，则$F$与$\dfrac{1}{(\Delta t)^{2}}$应满足的关系式为                 。（可用$m$、$d$、$s$、$\Delta t$等字母表示）

小车通过光电门的速度$v= \dfrac{d}{\Delta t}$

由匀变速直线运动规律$v^{2}=2as$

若满足牛顿第二定律则有$F=ma$

解得$F=\dfrac{md^{2}}{2s{(\Delta t)}^{2}}$

小红研究组测出木块静止时遮光片右端距光电门左端的位移$s$，由遮光片宽度$d$和挡光时间$\Delta t$求出滑块的速度大小$v$，并算出$v^{2}$，然后作出的$F-v^{2}$图像如图乙所示，根据图像可求得动摩擦因数$\mu =$                 。（可用$a$、$b$、$g$、$s$等字母表示）

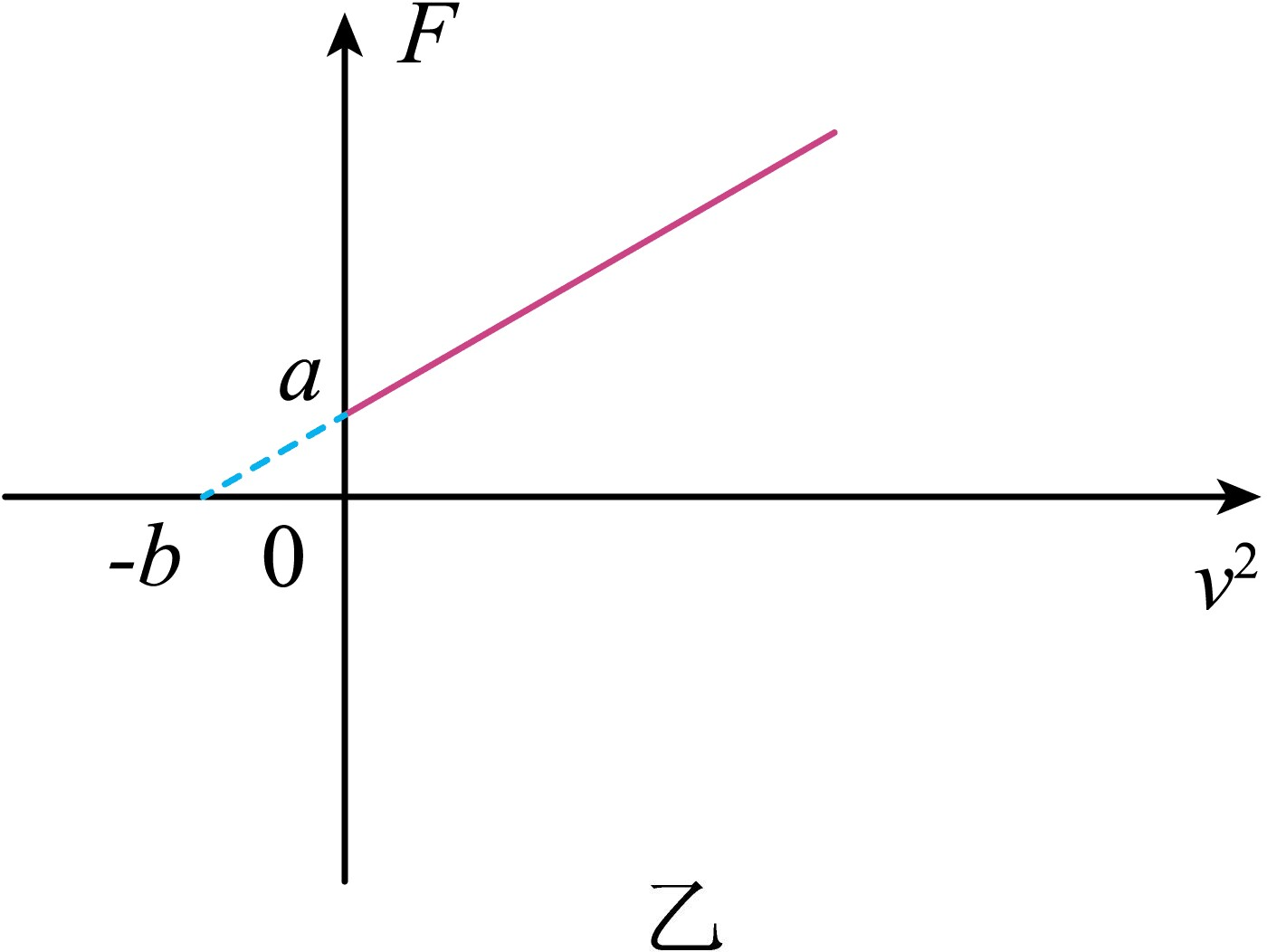
根据动能定理可得$(F-\mu mg)s= \dfrac{1}{2}mv^{2}$

解得$F=\dfrac{mv^{2}}{2s}+\mu mg$

结合图像可得$\dfrac{a}{b}=\dfrac{m}{2s}$、$\mu mg=a$

联立解得$\mu=\dfrac{b}{2gs}$