| 动能定理解决多过程问题 题目答案及解析
稿件来源:高途
| 动能定理解决多过程问题题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.7 动能和动能定理
动能定理解决多过程问题
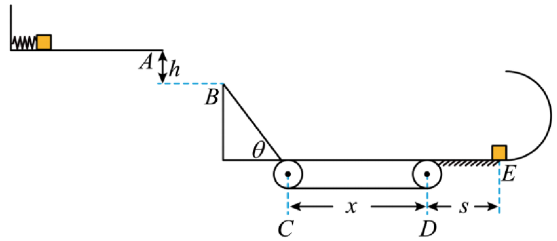
如图为研究能量间转化设计的装置。一处于压缩锁定状态的轻质弹簧置于光滑水平台面上,储存的弹性势能大小为$1\;\rm J$,弹簧左侧与墙壁相连,右侧与质量$m=500\;\rm g$的小物块接触但不固连。某时刻解除弹簧锁定,弹簧恢复原长将小物块弹开,让其从平台最右端$A$点离开后恰好能无碰撞地落在右下方的光滑斜面的顶端$B$点,斜面长度$L=\dfrac{2}{3}\sqrt{3}\;\rm \text{m}$倾角$\theta=60^\circ $,小物块沿斜面运动到底端$C$点后滑上长$x=1.3\;\rm m$的传送带,传送带顺时针匀速转动的速度为$8\;\rm m/s$,不考虑从斜面滑到传送带上的能量损失。从传送带右端离开后小物块滑行一段水平轨道$DE$后又冲上一半径$R=0.5\;\rm m$的光滑圆形轨道内侧,其中竖直圆轨道在$E$处错开不闭合。已知小物块与传送带及$DE$段轨道间的动摩擦因数均为$0.5$,$\sin 60{^\circ}=\dfrac{\sqrt{3}}{2}$,$\cos 60^\circ =0.5$,$g=10\;\rm m/s^{2}$,不计空气阻力,求:
小物块做平抛运动到$B$点时速度大小、$AB$间的高度差$h$;
$v_{B}=4\\;\\rm m/s$,$h=0.6\\;\\rm m$
"]]小物块离开弹簧过程,由能量守恒定律得$Ep=\dfrac{1}{2}mv_{0}^{2}$
小物块离开弹簧后刚滑到$A$点的速度$v_{0}=2\;\rm m/s$
小物块离开$A$点后做平抛运动,恰好能无碰撞地落在右下方的光滑斜面的顶端$B$点,即在$B$点的速度方向沿斜面,则$\dfrac{v_{0}}{v_{B}}=\cos\theta$
解得$v_{B}=4\;\rm m/s$
又$\dfrac{v_{0}}{v_{y}}=\tan\theta$,$v_{y}^{2}=2gh$
解得$h=0.6\;\rm m$
若小物块恰好能到达半圆形轨道的最高点,则$DE$段的距离$s$为多少;
$2.4\\;\\rm m$
"]]小物块由$B$运动到$C$,由动能定理$mgL\sin\theta=\dfrac{1}{2}mv_{C}^{2}- \dfrac{1}{2}mv_{B}^{2}$
解得$v_{C}=6\;\rm m/s$
小物块在传送带上运动到$D$点时,有$v_{D}^{2}-v_{C}^{2}=2\mu gx$
解得$v_{D}=7\;\rm m/s \lt 8\;\rm m/s$
小物块运动到$E$点时,有$v_{E}^{2}-v_{D}^{2}=-2\mu gs$
小物块恰好能到达半圆形轨道的最高点,设最高点速度为$v_{m}$,有$mg=m\dfrac{v_{\text{m}}^{2}}{R}$
由动能定理可得$\dfrac{1}{2}mv_{\text{m}}^{2}-\dfrac{1}{2}mv_{E}^{2}=- 2mgR$
解得$S=2.4\;\rm m$
若保证$DE$间的距离为第($2$)问所求结果不变,且将最右侧半圆形轨道半径调整为$1.25\;\rm m$,则当传送带顺时针转动的速度大小可变时,试讨论小物块最终停止时距离传送带右端$D$点的距离$l$与传送带运行的速度$v$之间的关系。
①$7\\;{\\rm m/s}\\leqslant v$,$l=0.1m$;②$0 \\leqslant v \\leqslant \\sqrt{23}\\;\\rm m/s$,$l=2.3\\;\\rm m$;③$\\sqrt{48} \\leqslant v \\leqslant 7\\left( {\\text{m}}/{\\text{s}} \\right)$,$l =\\dfrac{v^{2}}{10}-2\\;\\rm s$;④$\\sqrt{24} \\leqslant v \\lt \\sqrt{48}\\left( {\\text{m}}/{\\text{s}} \\right)$,$l=2\\;{\\rm s}- \\dfrac{v^{2}}{10}$;⑤$\\sqrt{23} \\leqslant v \\lt \\sqrt{24}\\left( {\\text{m}}/{\\text{s}} \\right)$,$l=\\dfrac{v^{2}}{10}$
"]]①将最右侧半圆形轨道半径调整为$1.25\;\rm m$,小物块无法到达最高点,当传送带速度$v\geqslant 7\;\rm m/s$,小物块在传送带上全程加速,到达$D$点的速度始终为$7\;\rm m/s$,由动能定理得
理可得$- mgh_{1}-\mu mgs=0-\dfrac{1}{2}mv_{D}^{2}$
解得$h_{1}=1.25\;\rm m$,小物块最高恰好上到圆心等高处,然后原路返回,再滑上传送带上不损失能量,根据能量守恒$\mu mgs_{1}=\dfrac{1}{2}mv_{D}^{2}$
解得$S_{1}=4.9\;\rm m$
解得$l=2\;\rm s-s_{1}=0.1\;\rm m$
②小物块在传送带上全程减速,有$v_{D}'^{2}-v_{C}^{2}=-2\mu gx$
解得$v_{D}=\sqrt{23}\;\rm \text{m}/\text{s}$
当传送带速度$0 \leqslant v \leqslant \sqrt{23}\;\rm \text{m}/\text{s}$
小物块到达$D$点的速度为$\sqrt{23}\;\rm \text{m/s}$,由动能定理可得$- \mu mgS_{2}=0-\dfrac{1}{2}mv_{D}^{2}$
解得$S_{2}=2.3\;\rm m\lt2.4\;\rm m$,$l=2.3\;\rm m$
③当传送带速度$\sqrt{23} \leqslant v \leqslant 7\left( {\text{m}}/{\text{s}} \right)$
小物块到达$D$点的速度为传送带速度$v$,由动能定理可得$- \mu mgs_{3}=0-\dfrac{1}{2}mv^{2}$
$s_{3}=\dfrac{v^{2}}{2\mu g}=\dfrac{v^{2}}{10}$
$\sqrt{48} \leqslant v \leqslant 7\left({\text{m}}/{\text{s}} \right)$,$l=\dfrac{v^{2}}{10}-2\;\rm s$
$\sqrt{24} \leqslant v \lt \sqrt{48}\left({\text{m}}/{\text{s}} \right)$,$l=2\;\rm s-\dfrac{v^{2}}{10}$
$\sqrt{23} \leqslant v \lt \sqrt{24}\left({\text{m}}/{\text{s}} \right)$,$l=\dfrac{v^{2}}{10}$
| 动能定理解决多过程问题题目答案及解析(完整版)
