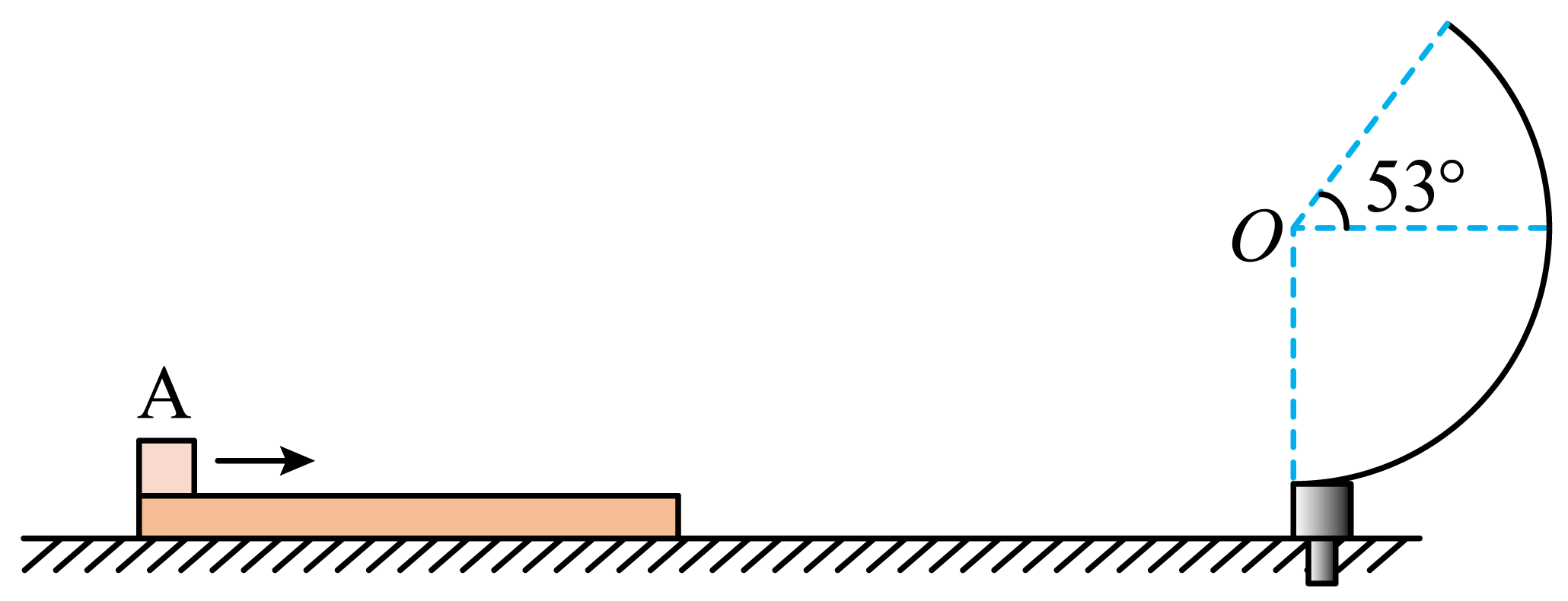
给予物块$A$一方向水平向右，大小$I_{1}=8\;\rm N⋅s$的冲量，

①在水平轨道上对$A$施加一方向水平向右，大小$F=12\;\rm N$的恒力，求物块刚进入圆弧轨道时对轨道作用力的大小$N$；

②物块进入圆弧轨道后撤去$F$，若要确保物块$A$在到达圆弧轨道上端点前不会脱离轨道，求$F$的最小值$F_{m}$。

①$N=72\\;\\rm N$；②$F_{m}=16\\;\\rm N$

①给予物块$A$一方向水平向右，大小$I_{1}=8\;\rm N ⋅ s$的冲量后，物块速度为$v_{1}$，有$I_{1}=mv_{1}$

解得$v_{1}=4\;\rm m/s$

物块$A$向右运动，由动能定理可知，$(F-mg\mu)L=\dfrac{1}{2}m\left( v^{2}-v_{1}^{2} \right)$

解得$v=2\sqrt{13}\;\rm \text{m/s}$

由牛顿第二定律，$F_{支}-mg=m\dfrac{v^{2}}{R}$

由牛顿第三定律，得$N=F_{支}=72\;\rm N$

②若能达到圆轨道上端点，该处速度必须满足$m\dfrac{v^{2}}{R} \geqslant mg\cos\theta$

解得$v\geqslant 4\;\rm m/s$

由动能定理可得$(F-mg\mu)L-mgR\left( 1+\cos\theta \right)=\dfrac{1}{2}m\left( v^{2}-v_{1}^{2} \right)$

解得$F_{m}=16\;\rm N$

给予物块$A$一方向水平向右，大小$I_{2}=26\;\rm N⋅s$的冲量，

①求物块$A$在整个运动过程中相对水平轨道的最大高度$H$；

②物块$A$在该最大高度处炸裂成质量$1:3$的两小物块$B$和$C$，其中一块速度方向水平向左。若$B$和$C$仅有一个平抛直接落在水平轨道上（不考虑多次反弹），求爆炸过程中机械能增加量$E$的范围。

①$H=4.05\\;\\rm m$；②$12\\;{\\rm J}\\lt E\\lt 48\\;\\rm J$

给予物块$A$一冲量$I_{2}$后，$I_{2}=mv_{2}$

解得$v_{2}=13\;\rm m/s$

①物块到达圆轨道最上端处的速度为$- mg\mu L-mgR\left( 1+\cos\theta \right)=\dfrac{1}{2}m\left( v^{2}-v_{2}^{2} \right)$

解得此时$v=5\;\rm m/s$

脱轨后物块做斜抛运动，$H=\dfrac{\left( v\cos\theta \right)^{2}}{2g}+R\left( 1+\cos\theta \right)$

所以$H=4.05\;\rm m$

②物块在高点处水平方向速度为$v_{A}=v\sin\theta=4\;\rm m/s$

水平方向$x=v\sin\theta\dfrac{v\cos\theta}{g}=1.2\;\rm \text{m}$

由动量守恒$mv_{x}=\dfrac{3}{4}mv_{1}+\dfrac{1}{4}mv_{2}$

能量改变为$E=\dfrac{1}{2} \cdot \dfrac{3}{4}mv_{1}^{2}+\dfrac{1}{2} \cdot \dfrac{1}{4}mv_{2}^{2}-\dfrac{1}{2} \cdot mv_{x}^{2}=3\left( v_{1}-4 \right)^{2}$

图像如下

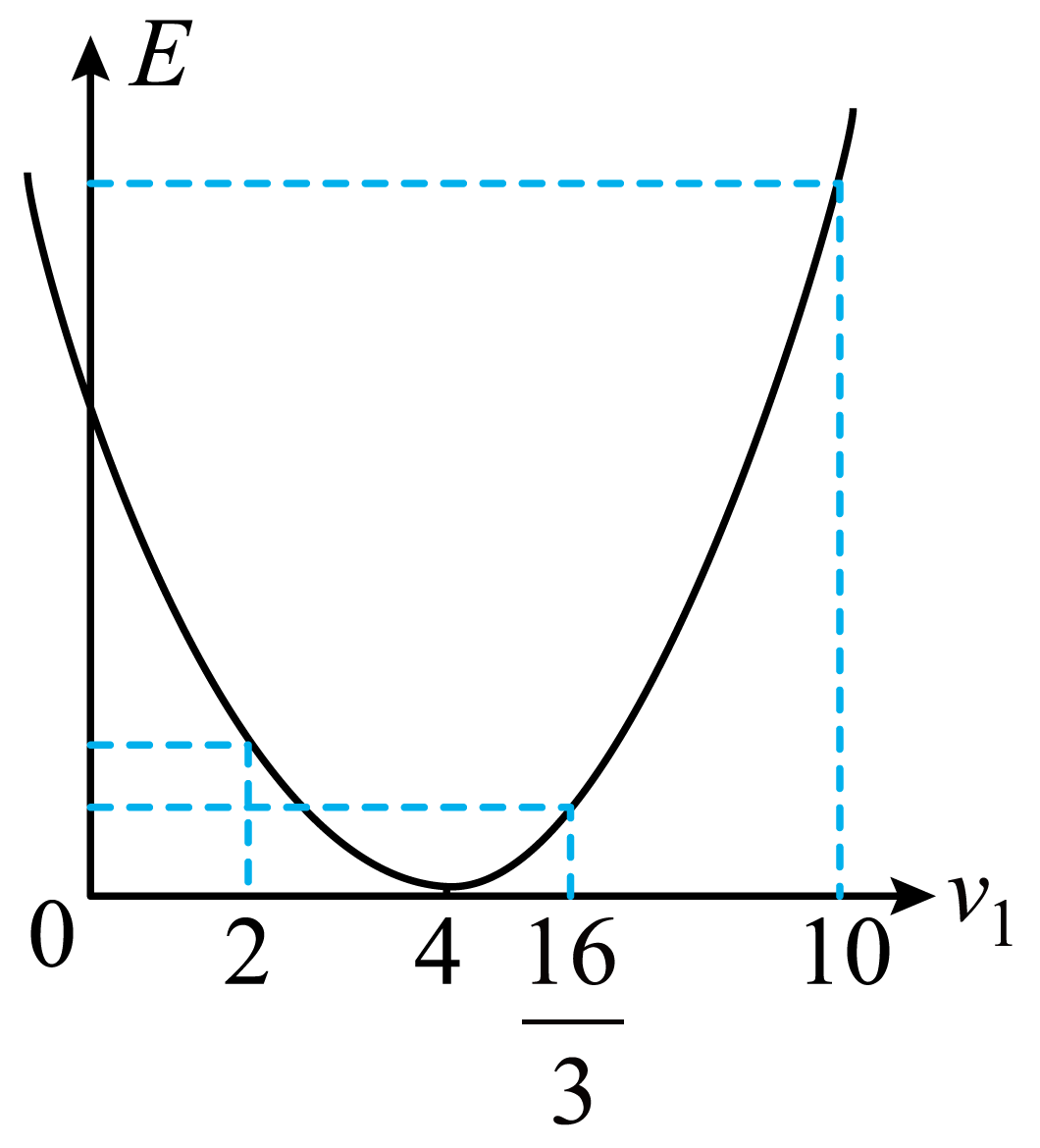
情况$1$：$C$能落板上，则$0\lt v_{1}\lt 10\;\rm m/s$

所以$-14\;{\rm m/s}\lt v_{2}\lt 16\;\rm m/s$

为满足要求$-14\;{\rm m/s}\lt v_{2}\lt 0$，则有$\dfrac{16}{3}\;\text{m}/\text{s}\lt v_{1} \lt 10\;\rm \text{m}/\text{s}$

或$0\lt v_{2}\lt 10\;\rm m/s$，解得$0\lt v_{1}\lt 2\;\rm m/s$

结合图像可知$\dfrac{16}{3}\;\text{J} \lt E \lt 108\;\rm \text{J}$

情况$2$：$B$落板上，由$0\lt v_{2}\lt10\;\rm m/s$可求得$2\; \text{m}/\text{s} \lt v_{1} \lt \dfrac{16}{3}\text{m}/\text{s}$，此时$C$也落板上，舍去。

综上所述，$\dfrac{16}{3}\;\text{J} \lt E \lt 108\;\rm \text{J}$