| 动能定理解决多过程问题 题目答案及解析
稿件来源:高途
| 动能定理解决多过程问题题目答案及解析如下,仅供参考!
必修2
第七章 机械能守恒定律
7.7 动能和动能定理
动能定理解决多过程问题
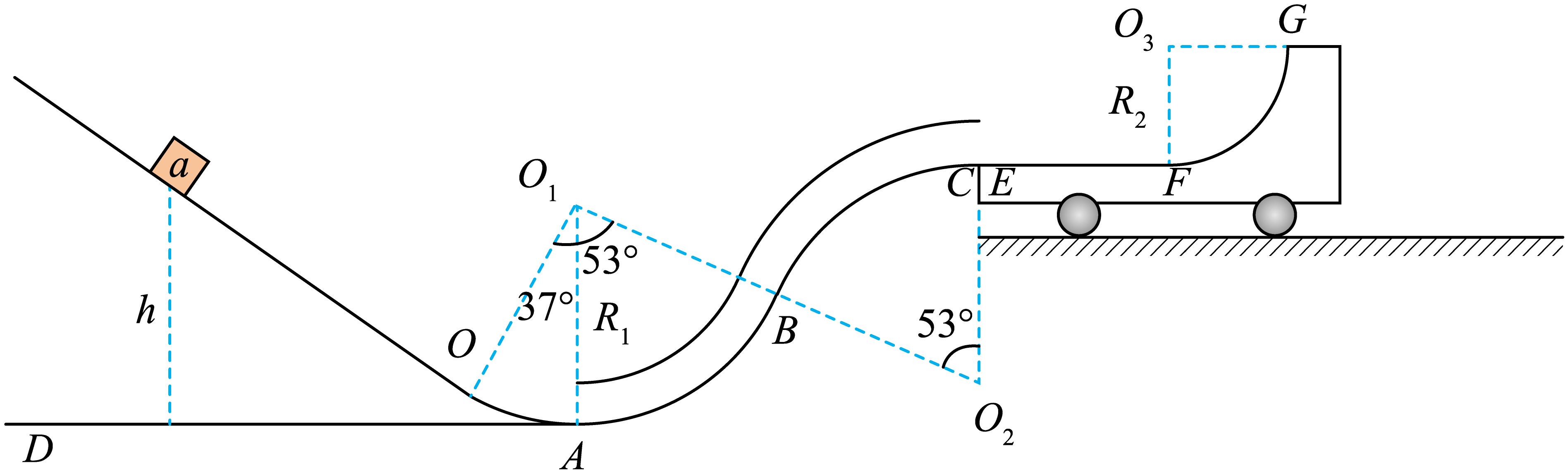
某装置的竖直截面如图所示,足够长的光滑倾斜轨道与圆弧$OABC$轨道平滑连接,$OABC$管道与平面$AD$相切于$A$点,$OABC$管道半径$R_{1}=0.5\;\rm m$,倾斜轨道上有一滑块$a$可从任意高度$h$($h$为滑块$a$到$AD$平面的竖直高度)由静止开始下滑($h$可变),滑块$a$尺寸略小于管道内径,管道$C$点与小车平面等高,小车左端紧靠管道$C$点,小车由水平轨道$EF$与四分之一圆弧轨道$FG$组成,水平轨道$L_{EF}=0.8\;\rm m$,圆弧轨道$FG$半径$R_{2}=0.2\;\rm m$,圆弧$AB$,$BC$对应的圆心角均$53^\circ $,圆弧$OA$对应的圆心角为$37^\circ $。滑块$a$与$EF$轨道间的动摩擦因数$\mu =0.5$,滑块$a$质量$m_{1}=0.1\;\rm kg$,小车质量$m_{2}=0.4\;\rm kg$。其它轨道均光滑,滑块可视为质点,不计空气阻力,$g$取$10\;\rm m/s^{2}$($\sin 53^\circ =0.8$,$\cos 53^\circ =0.6$)求:
滑块$a$从斜面静止下滑恰能滑到$C$点,求滑块下滑高度$h_{1}$;
$0.4\\;\\rm m$
"]]物体恰能滑到$C$点$v_{c}=0$
根据动能定理有$m_{1}gh_{1}-m_{1}g ⋅ 2R_{1}(1-\cos 53^\circ )=0$
解得$h_{1}=0.4\;\rm m$
若小车没有固定在平面上,平面光滑且足够长,滑块$a$滑上小车恰能到达$F$点,求滑块下滑高度$h_{2}$;
$h_{2}=0.9\\;\\rm m$
"]]恰能到达$F$点,由动量守恒得$m_{1}v_{c}=(m_{1}+m_{2})v_{共}$
由能量守恒得$\mu m_{1}gL_{EF}=\dfrac{1}{2}m_{1}{v_{c}}^{2}-\dfrac{1}{2}\left( m_{1}+m_{2} \right){v_{共}}^{2}$
解得$v_{c}=\sqrt{10}\;\rm \text{m}/\text{s}$
由动能定理得$m_{1}gh_{2}-2m_{1}gR_{1}\left( 1-\cos 53{^\circ} \right)=\dfrac{1}{2}m_{1}v_{c}^{2}$
解得$h_{2}=0.9\;\rm m$
若小车没有固定在平面上,半面光滑且足够长,滑块$a$能滑上小车并且不会滑离小车,求滑块下滑高度$h$的范围。
$0.4\\;{\\rm m}\\leqslant h\\leqslant 1.15\\;\\rm m$
"]]①物体滑上小车$v_{c}=0$此时$h=0.4\;\rm m$
②物体恰能到达$G$点,由动量守恒得$m_{1}v_{c_2}=(m_{1}+m_{2})v_{1}$
由能量守恒得$\mu m_{1}gL_{EF}+m_{1}gR_{2}=\dfrac{1}{2}m_{1}{v_{c_2}}^{2}-\dfrac{1}{2}\left( m_{1}+m_{2} \right){v_{1}}^{2}$
解得$v_{c_2}=\sqrt{15}\;\rm \text{m}/\text{s}$
由动能定理得$m_{1}gh_{3}-2m_{1}gR_{1}\left( 1-\cos 53{^\circ} \right)=\dfrac{1}{2}m_{1}{v_{c2}}^{2}$
解得$h_{3}=1.15\;\rm m$
③物体返回$EF$恰好不从$E$点滑出,由动量守恒得$m_{1}v_{c_3}=(m_{1}+m_{2})v_{2}$
由能量守恒得$2 \mu m_{1}gL_{EF}=\dfrac{1}{2}m_{1}{v_{c_3}}^{2}-\dfrac{1}{2}\left( m_{1}+m_{2} \right){v_{2}}^{2}$
解得$v_{c_3}=\sqrt{20}\;\rm \text{m}/\text{s}$
由动能定理得$m_{1}gh_{4}-2m_{1}gR_{1}\left( 1-\cos 53{^\circ} \right)=\dfrac{1}{2}m_{1}{v_{c_3}}^{2}$
解得$h_{4}=1.4\;\rm m$
综上所述$0.4\;{\rm m}\leqslant h\leqslant 1.15\;\rm m$
| 动能定理解决多过程问题题目答案及解析(完整版)
