已知${{\text{H}}_{2}}\left( \text{g} \right)$、${{\text{C}}_{2}}{{\text{H}}_{6}}\left( \text{g} \right)$、${{\text{C}}_{2}}{{\text{H}}_{4}}\left( \text{g} \right)$的燃烧热分别为$-285.8\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$、$-1560\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$、$-1411\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$。计算$\Delta {{ {H}}_{\text{3}}}=$                。

$-136.8\\;\\rm \\text{kJ}\\cdot \\text{mo}{{\\text{l}}^{-1}}$

已知燃烧热的热化学方程式：①${\rm{{{H}}_{{2}}}{(g)+}\dfrac{{1}}{{2}}{{{O}}_{{2}}}{(g)=}{{{H}}_{{2}}}{O(l)}}\qquad \Delta { H=}\rm-{285}{.8\;\rm kJ}\cdot {mo}{{{l}}^{-1}}$；

②${\rm{{{C}}_{{2}}}{{{H}}_{{6}}}{(g)+}\dfrac{{7}}{{2}}{{{O}}_{{2}}}{(g)=2C}{{{O}}_{{2}}}{(g)+3}{{{H}}_{{2}}}{O(l)}}\qquad \Delta{ H=}\rm-{1560\;\rm kJ}\cdot {mo}{{{l}}^{-1}}$；

③${\rm{{{C}}_{{2}}}{{{H}}_{{4}}}{(g)+3}{{{O}}_{{2}}}{(g)=2C}{{{O}}_{{2}}}{(g)+2}{{{H}}_{{2}}}{O(l)}}\qquad \Delta{ H=}\rm-{1411\;\rm kJ}\cdot {mo}{{{l}}^{-1}}$，根据盖斯定律，由①$\rm +$③ $\rm -$ ②可得$\rm{{{C}}_{2}}{{{H}}_{4}}\left( {g} \right)+{{{H}}_{2}}\left( {g} \right)\rightleftharpoons {{{C}}_{2}}{{{H}}_{6}}\left( {g} \right)$，$\Delta{{{H}}_{{3}}}=-285.8\;\rm {kJ}\cdot {mo}{{{l}}^{-1}}+(-1411\;\rm {kJ}\cdot {mo}{{{l}}^{-1}})-(-1560\;\rm {kJ}\cdot {mo}{{{l}}^{-1}})=-136.8\;\rm {kJ}\cdot {mo}{{{l}}^{-1}}$；

向体积可变的密闭容器中加入$\rm 1\;\rm mol {{\text{ C}}_{3}}{{\text{H}}_{8}}\left( \text{g} \right)$，分别在$\rm 0.1\;MPa$和$\rm 0.01\;MPa$下，不同温度时，发生上述反应，反应达到平衡时，丙烷的转化率及$\rm 0.1\;MPa$下${{\text{C}}_{3}}{{\text{H}}_{8}}\left( \text{g} \right)$和${{\text{C}}_{3}}{{\text{H}}_{6}}\left( \text{g} \right)$的物质的量分数随温度变化的曲线如图所示：

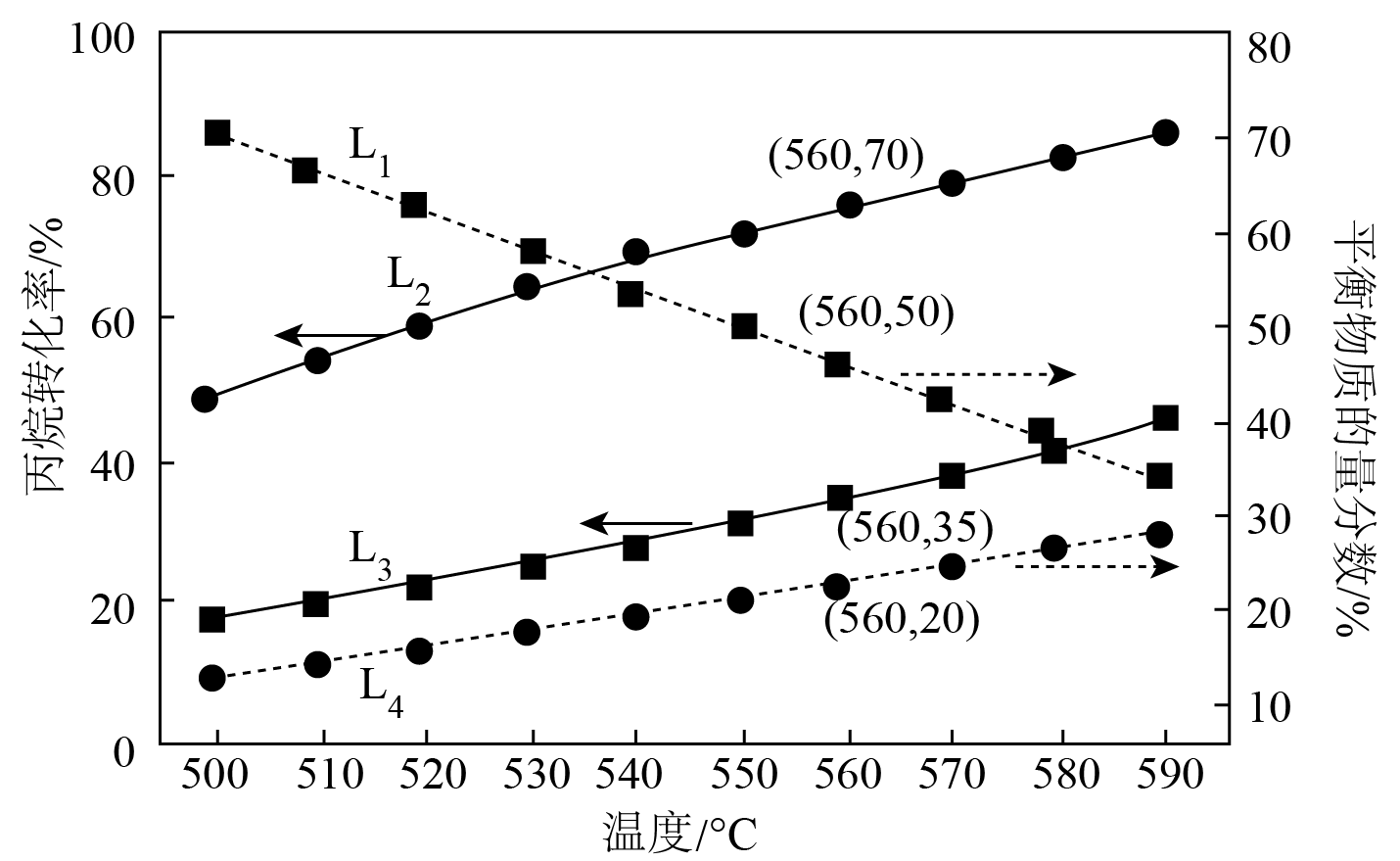
①${{\text{L}}_{2}}$曲线所在的压强为                $\rm MPa$；${{\text{L}}_{1}}$代表                物质在$\rm 0.1\;MPa$下的物质的量分数随温度变化的曲线，判断理由为                ；

②若在$\rm 560\;\rm ^\circ\rm C$，$\rm 0.1\;MPa$下反应进行$n$ $\rm min$时反应达到平衡，反应ⅰ用${{\text{C}}_{3}}{{\text{H}}_{8}}\left( \text{g} \right)$表示$ 0\sim n$ $\rm min$时间内的平均反应速率为                $\;\rm \text{mol}\cdot {{\min }^{-1}}$；反应ⅰ的压强平衡常数${{K}_{\text{p}}}$为                ${\rm MPa}({{K}_{\text{p}}}$为用平衡分压代替平衡浓度计算的平衡常数，保留三位有效数字$\rm )$。

$\\rm 0.01$；${{\\text{C}}_{3}}{{\\text{H}}_{8}}\\left( \\text{g} \\right)$；反应$\\rm i$为吸热反应，升高温度，平衡正向移动，${{\\text{C}}_{3}}{{\\text{H}}_{8}}\\left( \\text{g} \\right)$物质的量分数减小；$\\dfrac{\\text{0}\\text{.35}}{ {n}}$；$\\text{0}.00646$

①对于反应$\rm i$和$\rm ii$，正反应是气体体积增大的反应，减小压强，平衡正向移动，丙烷转化率增大，所以${{\text{L}}_{2}}$曲线所在压强为$\rm 0.01\;MPa$，${{\text{L}}_{3}}$去哦在曲线表示的压强为$\rm 0.1\;MPa$；反应$\rm i$是吸热反应，升高温度，平衡正向移动，${{\text{C}}_{3}}{{\text{H}}_{8}}\left( \text{g} \right)$物质的量分数减小，${{\text{C}}_{3}}{{\text{H}}_{6}}\left( \text{g} \right)$物质的量分数增大，所以${{\text{L}}_{1}}$代表${{\text{C}}_{3}}{{\text{H}}_{8}}\left( \text{g} \right)$物质在$\rm 0.1\;MPa$下的物质的量分数随温度变化的曲线，理由是反应$\rm i$为吸热反应，升高温度，平衡正向移动，${{\text{C}}_{3}}{{\text{H}}_{8}}\left( \text{g} \right)$物质的量分数减小，则${{\text{L}}_{4}}$代表${{\text{C}}_{3}}{{\text{H}}_{6}}\left( \text{g} \right)$的物质的量分数随温度变化的曲线；

②在$\rm 560\;\rm ^\circ\rm C$，$\rm 0.1\;MPa$下，起始加入${1\;\rm mol}\rm \;{{{ C}}_{{3}}}{{{H}}_{{8}}}$，由图可知平衡时丙烷转化率为$\rm 35\%$，则反应的$ {n}\left(\rm {{{C}}_{{3}}}{{{H}}_{{8}}} \right){=1\rm \; mol}\times {35 } \% { =0}{.35\rm \; mol}$。反应$\rm i$用$\rm {{{C}}_{{3}}}{{{H}}_{{8}}}$表示$ 0 - n$ $\rm min$时间内的平均反应速率$ {v=}\dfrac{{0}{.35\rm \; mol}}{{n \;\rm min}}=\dfrac{{0}{.35}}{ {n}}{ \rm \;mol}\cdot \rm {mi}{{{n}}^{-1}}$；平衡时$ {n}\left(\rm {{{C}}_{{3}}}{{{H}}_{{8}}} \right) {=(1}-{0}{.35)\;\rm mol=0}{.65\rm \; mol}$，由曲线$\rm {{{L}}_{1}}$可知，在$\rm 560\;\rm ^\circ\rm C$，$\rm 0.1\;MPa$下$\rm {{{C}}_{3}}{{{H}}_{8}}\left( {g} \right)$的物质的量分数为$\rm 50\\%$，则${{ {n}}_总{}}{=0}{.65\;\rm mol}\times {2=1}{.3\;\rm mol}$，由曲线${\rm {{L}}_{4}}$可知，在$\rm 560\;\rm ^\circ\rm C$，$\rm 0.1\;MPa$下$\rm {\rm {{C}}_{3}}{{{H}}_{6}}\left( {g} \right)$的物质的量分数为$\rm 20\%$，则${n(}{{\rm {C}}_{3}}{\rm {{H}}_{6}})=1.3\;\rm {mol}\times 20\%{=0}{.26\;\rm mol}$，由三段式$\begin{matrix} {} &\rm {{{C}}_{3}}{{{H}}_{8}}\left( {g} \right) &\rm \rightleftharpoons & \rm {{{C}}_{3}}{{{H}}_{6}}\left( {g} \right) & + &\rm {{{H}}_{2}}\left( {g} \right) \\起始 {\rm mol} & 1 & {} & 0 & {} & 0 \\ 变化{\rm mol} & 0.26 & {} & 0.26 & {} & 0.26 \\ 平衡{\rm mol} & 0.74 & {} & 0.26 & {} & 0.26 \\ \end{matrix}$，$\begin{matrix} {} & \rm {{{C}}_{3}}{{{H}}_{8}}\left( {g} \right) & \rightleftharpoons &\rm {C}{{{H}}_{4}}\left( {g} \right) & + &\rm {{{C}}_{2}}{{{H}}_{4}}\left( {g} \right) \\起始 {\rm mol} & 0.74 & {} & 0 & {} & 0 \\ 变化{\rm mol} & 0.09 & {} & 0.09 & {} & 0.09 \\ 平衡{\rm mol} & 0.65 & {} & 0.09 & {} & 0.09 \\ \end{matrix}$，$\begin{matrix} {} &\rm {{{C}}_{2}}{{{H}}_{4}}\left( {g} \right) & + &\rm {{{H}}_{2}}\left( {g} \right) & \rightleftharpoons &\rm {{{C}}_{2}}{{{H}}_{6}}\left( {g} \right) \\起始 {\rm mol} & 0.09 & {} & {0}{.26} & {} & 0 \\变化 {\rm mol} & {x} & {} & {x} & {} & {x} \\平衡 {\rm mol} & 0.09-{x} & {} & {0}{.26}-{x} & {} & {x} \\ \end{matrix}$，则${{{n}}_总{}}{=(0}{.65}+0.26+0.09+0.09-{x}+0.26-{x}+{x}){\rm \;mol=1}{.3\;\rm mol}$，解得${x=0}{.05\;\rm mol}$，${p(}{{\rm {C}}_{{3}}}{{{\rm H}}_{{8}}}{)=}\dfrac{{0}{.65\;\rm mol}}{{1}{.3\;\rm mol}}\times {0}{.1\rm \;MPa}$，${p(}{{{\rm C}}_{{3}}}{{\rm {H}}_{{6}}}{)=}\dfrac{{0}{.26\;\rm mol}}{{1}{.3\;\rm mol}}\times {0}{.1\rm \;MPa}$，${p(}{{\rm {H}}_{{2}}}{)=}\dfrac{{(0}{.26}-{0}{.05)\rm \;mol}}{1.3\;\rm {mol}}\times {0}{.1\rm \;MPa=}\dfrac{{0}{.2}1\;\rm {mol}}{1.3\;\rm {mol}}\times {0}{.1\rm \;MPa}$，压强平衡常数${{{K}}_{\rm {p}}}=\dfrac{{p(}{{{\rm C}}_{{3}}}{{\rm {H}}_{{6}}}{)}\times {p(}{{{\rm H}}_{{2}}}{)}}{{p(}{{\rm {C}}_{{3}}}{{\rm {H}}_{{8}}}{)}}=\dfrac{\dfrac{{0}{.26}}{{1}{.3}}\times {0}{.1}\times \dfrac{{0}{.21}}{{1}{.3}}\times {0}{.1}}{\dfrac{{0}{.65}}{{1}{.3}}\times {0}{.1}}=\dfrac{0.26\times 0.21\times 0.1}{0.65\times 1.3}\approx {0}{.00646\rm \;MPa}$；

在中性或碱性环境中，通过可再生电能进行$\text{C}{{\text{O}}_{2}}$电化学还原实现了高效合成丙烯，得到丙烯的电极为                $\rm ($填“阴极”或“阳极”$\rm )$；其电极反应式为                。

阴极；$\\text{3C}{{\\text{O}}_{\\text{2}}}\\text{+18}{{\\text{e}}^{-}}\\text{+12}{{\\text{H}}_{\\text{2}}}\\text{O=}{{\\text{C}}_{\\text{3}}}{{\\text{H}}_{\\text{6}}}\\text{+18O}{{\\text{H}}^{-}}$

$\text{C}{{\text{O}}_{2}}$电化学还原生成丙烯，碳元素化合价降低，发生还原反应，得到丙烯的电极为阴极，电极反应式为$\text{3C}{{\text{O}}_{\text{2}}}\text{+18}{{\text{e}}^{-}}\text{+12}{{\text{H}}_{\text{2}}}\text{O=}{{\text{C}}_{\text{3}}}{{\text{H}}_{\text{6}}}\text{+18O}{{\text{H}}^{-}}$。