科学研究人员通过“$\rm Sabatier$反应器”实现了将$\text{C}{{\text{O}}_{2}}$转化为$\text{C}{{\text{H}}_{4}}$，如图$\rm 1$是空间站中的循环过程示意图。

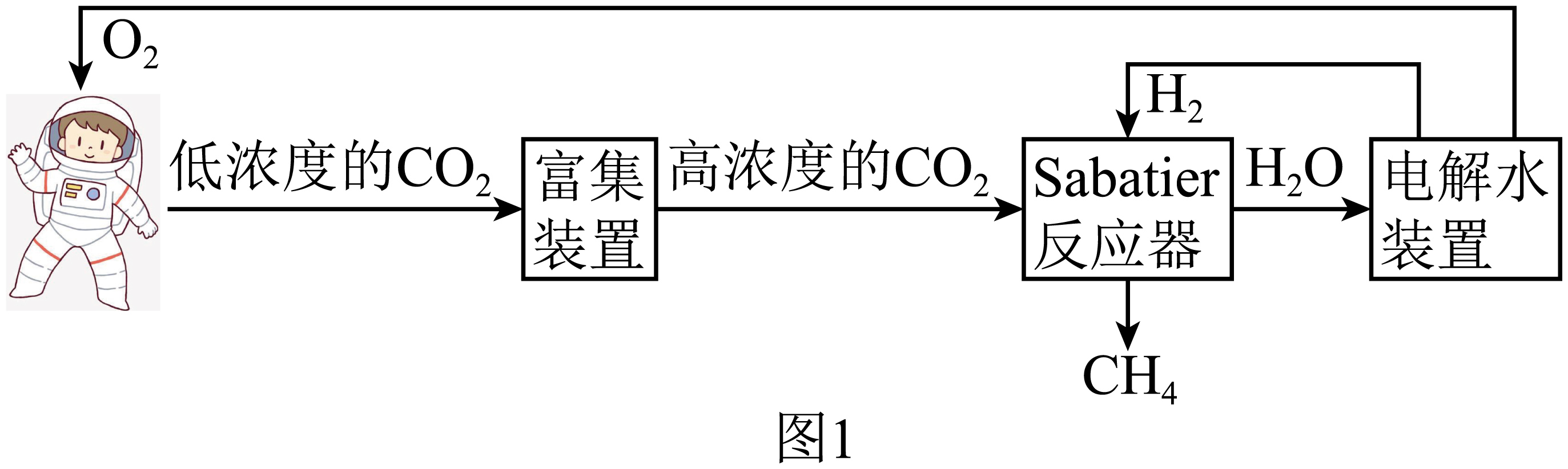
已知：某温度下，由处于标准状态的各种元素的指定单质生成标准状态的$\rm 1\;\rm mol$某纯物质的热效应，叫做该温度下该物质的标准摩尔生成热${{\Delta}_{{f}}}\text{H}_{{m}}^{\ominus }$。下表给出了几种物质在$\rm 298$ $\rm K$下的标准摩尔生成热，则“$\rm Sabatier$反应器”中发生反应的热化学方程式为                。

$\\text{C}{{\\text{O}}_{2}}(\\text{g})+4{{\\text{H}}_{2}}(\\text{g})\\rightleftharpoons \\text{C}{{\\text{H}}_{4}}(\\text{g})+2{{\\text{H}}_{2}}\\text{O}(\\text{g})\\quad \\Delta H=-164.98\\ \\text{kJ}\\cdot \\text{mo}{{\\text{l}}^{-1}}$  

由示意图可知，“$\rm Sabatier$反应器”中发生的反应为$\text{C}{{\text{O}}_{2}}(\text{g})+4{{\text{H}}_{2}}(\text{g})\rightleftharpoons \text{C}{{\text{H}}_{4}}(\text{g})+2{{\text{H}}_{2}}\text{O}(\text{g})$，根据题给数据，该反应的焓变$\Delta H=-74.85\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}+2\times \left( -241.82\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}} \right)-\left( -393.51\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}} \right)=-164.98\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$，故“$\rm Sabatier$反应器”中发生反应的热化学方程式为$\text{C}{{\text{O}}_{2}}(\text{g})+4{{\text{H}}_{2}}(\text{g})\rightleftharpoons \text{C}{{\text{H}}_{4}}(\text{g})+2{{\text{H}}_{2}}\text{O}(\text{g})\quad \Delta H=-164.98\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$；

写出一种有利于提高“$\rm Sabatier$反应器”中反应的转化率的措施                。

降低温度

“$\rm Sabatier$反应器”中反应为放热反应，适当降低温度，平衡正向移动，反应转化率提高，该反应为气体分子数减小的反应，适当增大压强，平衡正向移动，反应转化率提高；

Ⅱ．有机胺用于塑料加工

工业上可用对苯二胺加氢制备$\rm 1$，$\rm 4-$环己二胺，主要反应如下：

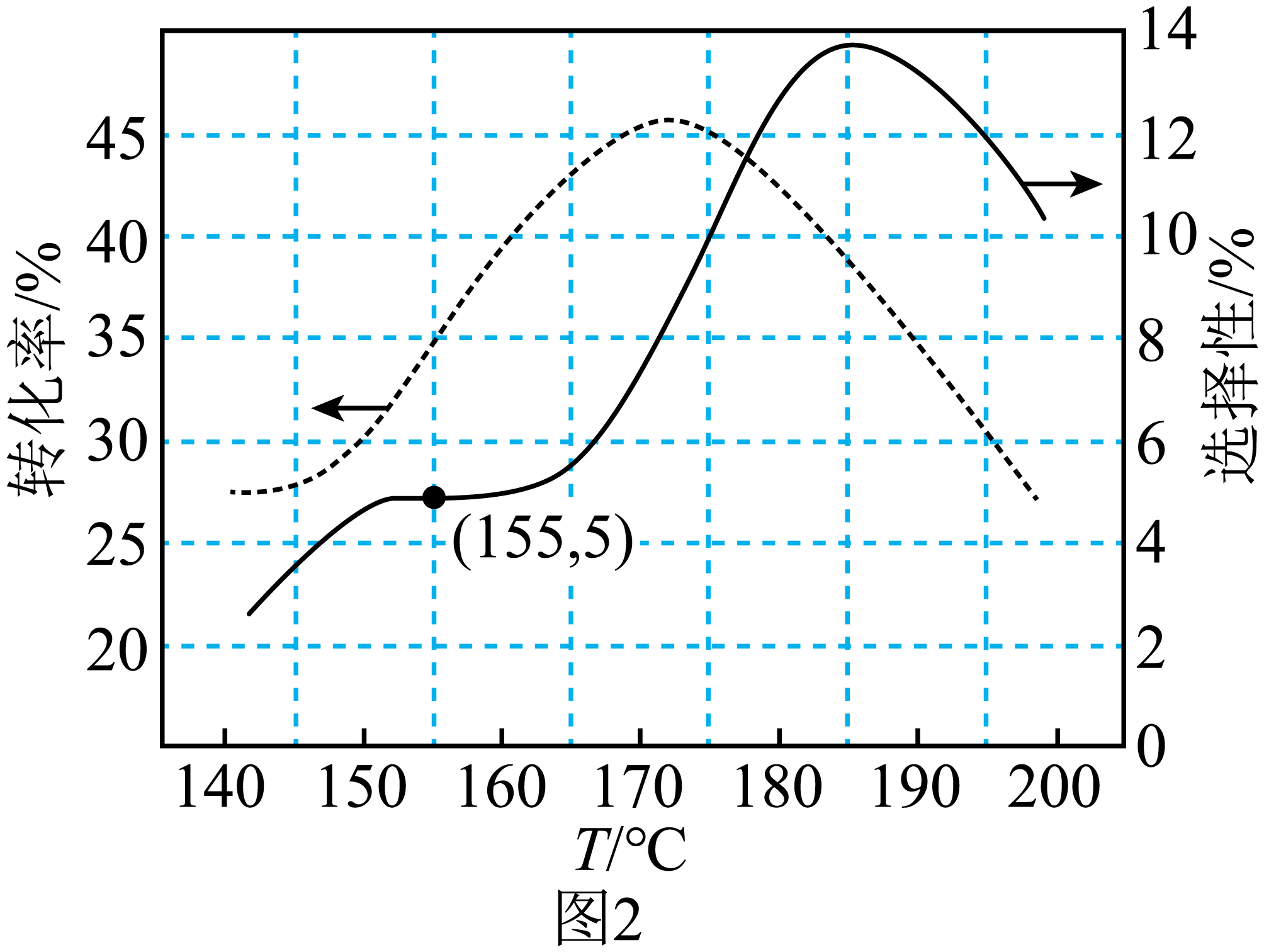
现取$\rm 4$ $\rm mol$对苯二胺，少量催化剂和一定量的氢气于反应釜中发生反应，$t\,\text{h}$后，对苯二胺的转化率以及$1,4-$环己二胺的选择性随温度变化如图$\rm 2$所示，则$0\sim t\ \text{h}$内，$155\ \text{ }{}^\circ \text{C}$时，$v(1,4-$环己二胺$\rm )=$                $\text{mol}\cdot {{\text{h}}^{-1}}\rm ($列出计算式$\rm )$。

$\\dfrac{4 \\times 35 \\% \\times 5 \\%}{t}$

$155\ \text{ }{}^\circ \text{C}$时，对苯二胺的转化率为$35\%$，产物$1,4-$环己二胺的选择性为$5\%$，所以$0\sim t\ \text{h}$内，$v(1,4-环己二胺)=\dfrac{4\times 35\%\times 5\%}{t}\ \text{mol}\cdot {{\text{h}}^{-1}}$；

当温度高于$185\text{ }{}^\circ \text{C}$时，对苯二胺的转化率以及$1,4-$环己二胺的选择性随温度升高均呈现下降趋势，试分析其原因可能为                。

催化剂活性降低

当温度高于$185\text{ }{}^\circ \text{C}$时，可能由于催化剂的活性降低或者发生了副反应而导致对苯二胺的转化率以及$\rm 1$，$\rm 4-$环己二胺的选择性随温度升高均呈现下降趋势；

Ⅲ．甲醇$\left( \text{C}{{\text{H}}_{3}}\text{OH} \right)$的制备

利用$\text{C}{{\text{O}}_{2}}$和${{\text{H}}_{2}}$合成甲醇主要涉及以下反应：

反应①：$\text{C}{{\text{O}}_{2}}(\text{g})+3{{\text{H}}_{2}}(\text{g})\rightleftharpoons \text{C}{{\text{H}}_{3}}\text{OH}(\text{g})+{{\text{H}}_{2}}\text{O}(\text{g})\quad \Delta {{H}_{1}}=-49\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

反应②：$\text{C}{{\text{O}}_{2}}(\text{g})+{{\text{H}}_{2}}(\text{g})\rightleftharpoons \text{CO}(\text{g})+{{\text{H}}_{2}}\text{O}(\text{g})\quad \Delta {{H}_{2}}=+41\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

在$\rm 1\;\rm L$的密闭容器中，加入催化剂，并投入$1\ \text{mol}\ \text{C}{{\text{O}}_{2}}$和$3\ \text{mol}\ {{\text{H}}_{2}}$发生上述两个反应，$\text{C}{{\text{O}}_{2}}$的平衡转化率和甲醇的选择性随温度的变化趋势如图$\rm 3$所示。

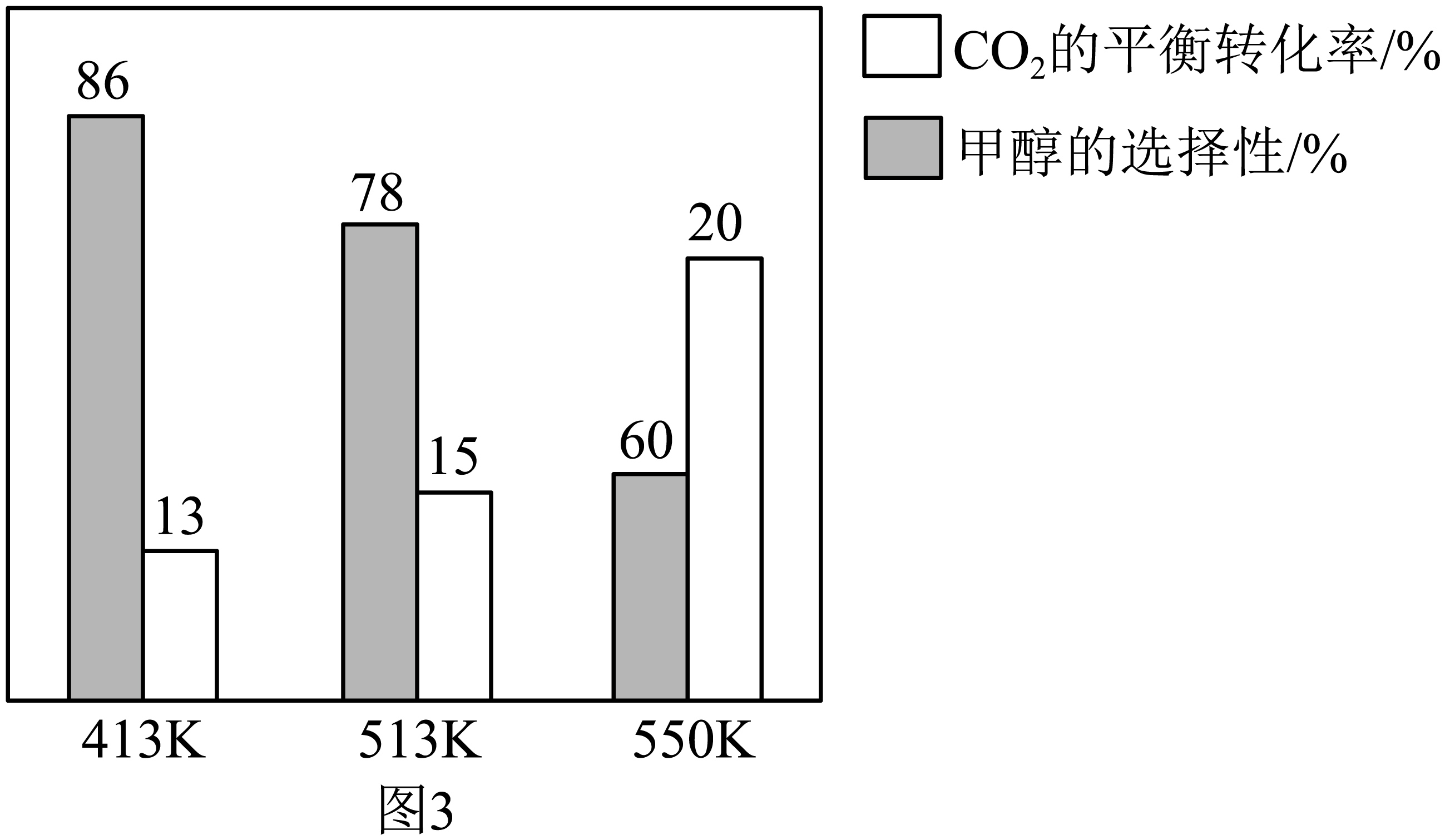
由图可知，达到平衡最适宜的温度为                $\rm ($填“$\rm 413$ $\rm K$”“$\rm 513$ $\rm K$”或“$\rm 550$ $\rm K$”$\rm )$。

$\\rm 513$ $\\rm K$

首先应选择甲醇的选择性比较高的温度，排除$550\ \text{K}$，$413\ \text{K}$和$\rm 513$ $\rm K$时甲醇的选择性和$\text{C}{{\text{O}}_{2}}$的转化率都相差不大，计算产率可知$\rm 413\ K$时$n\left( \text{C}{{\text{H}}_{3}}\text{OH} \right)=1\ \text{mol}\times 86\%\times 13\%=0.1118\ \text{mol}$，$513\ \text{K}$时$n\left( \text{C}{{\text{H}}_{3}}\text{OH} \right)=1\ \text{mol}\times 78\%\times 15\%=0.1170\ \text{mol}$，故最适宜的反应温度为$\rm 513$ $\rm K$；

$\rm 550$ $\rm K$时，若反应后体系的总压强为$p$，则反应①的${{K}_{\text{p}}}=$                $\rm ($列出计算式$\rm )$。

$\\dfrac{\\dfrac{0.12}{3.76}p\\cdot \\dfrac{0.2}{3.76}p}{\\dfrac{0.8}{3.76}p\\cdot {{\\left( \\dfrac{2.56}{3.76}p \\right)}^{3}}}$

第一步，结合图像信息，计算消耗$\text{C}{{\text{O}}_{2}}$的总的物质的量及生成$\rm CO$消耗的$\text{C}{{\text{O}}_{2}}$的物质的量，根据图像，$\rm 550K$时，$\text{C}{{\text{O}}_{2}}$的平衡转化率为$20\%$，则消耗$\text{C}{{\text{O}}_{2}}$的总的物质的量$=1\ \text{mol}\times 20\%=0.2\ \text{mol}$，平衡时$\text{C}{{\text{O}}_{2}}$的物质的量$=1\ \text{mol}-0.2\ \text{mol}=0.8\ \text{mol}$；甲醇的选择性为$60\%$，则生成甲醇消耗的$\text{C}{{\text{O}}_{2}}$的物质的量$=0.2\ \text{mol}\times 60\%=0.12\ \text{mol}$，那么生成$\rm CO$消耗的$\text{C}{{\text{O}}_{2}}$的物质的量$=0.2\ \text{mol}-0.12\ \text{mol}=0.08\ \text{mol}$。第二步，列三段式，计算各物质的分压，根据上述数据可以列出如下三段式：

$\begin{matrix} {} & \text{C}{{\text{O}}_{2}}\text{(g)} & + & \text{3}{{\text{H}}_{2}}\text{(g)} & \rightleftharpoons & \text{C}{{\text{H}}_{3}}\text{OH(g)} & + & {{\text{H}}_{2}}\text{O(g)} \\ 起始量\text{/mol} & 1 & {} & 3 & {} & 0 & {} & 0 \\ 转化量\text{/mol} & 0.12 & {} & 0.36 & {} & 0.12 & {} & 0.12 \\平衡量 \text{/mol} & 0.8 & {} & 2.56 & {} & 0.12 & {} & 0.2 \\ \end{matrix}$

$\begin{matrix} {} & \text{C}{{\text{O}}_{2}}\text{(g)} & + & {{\text{H}}_{2}}\text{(g)} & \rightleftharpoons & \text{CO(g)} & + & {{\text{H}}_{2}}\text{O(g)} \\ 起始量\text{/mol} & 1 & {} & 3 & {} & 0 & {} & 0 \\ 转化量\text{/mol} & 0.08 & {} & 0.08 & {} & 0.08 & {} & 0.08 \\平衡量 \text{/mol} & 0.8 & {} & 2.56 & {} & 0.08 & {} & 0.2 \\ \end{matrix}$

达到平衡后，体系中各物质的物质的量分别为$n\left( \text{C}{{\text{O}}_{2}} \right)=0.8\ \text{mol}$，$n\left( {{\text{H}}_{2}} \right)=2.56\ \text{mol}$，$n\left( \text{C}{{\text{H}}_{3}}\text{OH} \right)=0.12\ \text{mol}$，$n(\text{CO})=0.08\ \text{mol}$，$n\left( {{\text{H}}_{2}}\text{O} \right)=0.2\ \text{mol}$，则平衡时体系总物质的量为$(0.8+2.56+0.12+0.08+0.2)\ \text{mol}=3.76\ \text{mol}$，已知反应后体系的总压强为$p$，则达到平衡时，反应①中各物质的分压为$p\left( \text{C}{{\text{O}}_{\text{2}}} \right)=\dfrac{\text{0}\text{.8}}{\text{3}\text{.76}}p$，$p\left( {{\text{H}}_{\text{2}}} \right)=\dfrac{\text{2}\text{.56}}{\text{3}\text{.76}}p$，$p\left( \text{C}{{\text{H}}_{\text{3}}}\text{OH} \right)=\dfrac{0.12}{3.76}p$，$\dfrac{0.12}{3.76} p, p\left(\mathrm{H}_2 \mathrm{O}\right)=\dfrac{0.2}{3.76} p$，第三步，结合${{K}_{\text{p}}}$的计算公式，写出${{K}_{\text{p}}}$的表达式。反应①的${{K}_{\text{p}}}=\dfrac{p\left( \text{C}{{\text{H}}_{3}}\text{OH} \right)\cdot p\left( {{\text{H}}_{2}}\text{O} \right)}{p\left( \text{C}{{\text{O}}_{2}} \right)\cdot {{p}^{3}}\left( {{\text{H}}_{2}} \right)}=\dfrac{\dfrac{0.12}{3.76}p\cdot \dfrac{0.2}{3.76}p}{\dfrac{0.8}{3.76}p\cdot {{\left( \dfrac{2.56}{3.76}{p} \right)}^{3}}}$；

Ⅳ．甲酸$(\text{HCOOH})$的制备

工业上制备甲酸的反应为$\text{C}{{\text{O}}_{2}}(\text{g})+{{\text{H}}_{2}}(\text{g})\rightleftharpoons \text{HCOOH}(\text{g})$，该反应的速率方程$v=k\cdot c\left( \text{C}{{\text{O}}_{2}} \right)\cdot c\left( {{\text{H}}_{2}} \right)$。

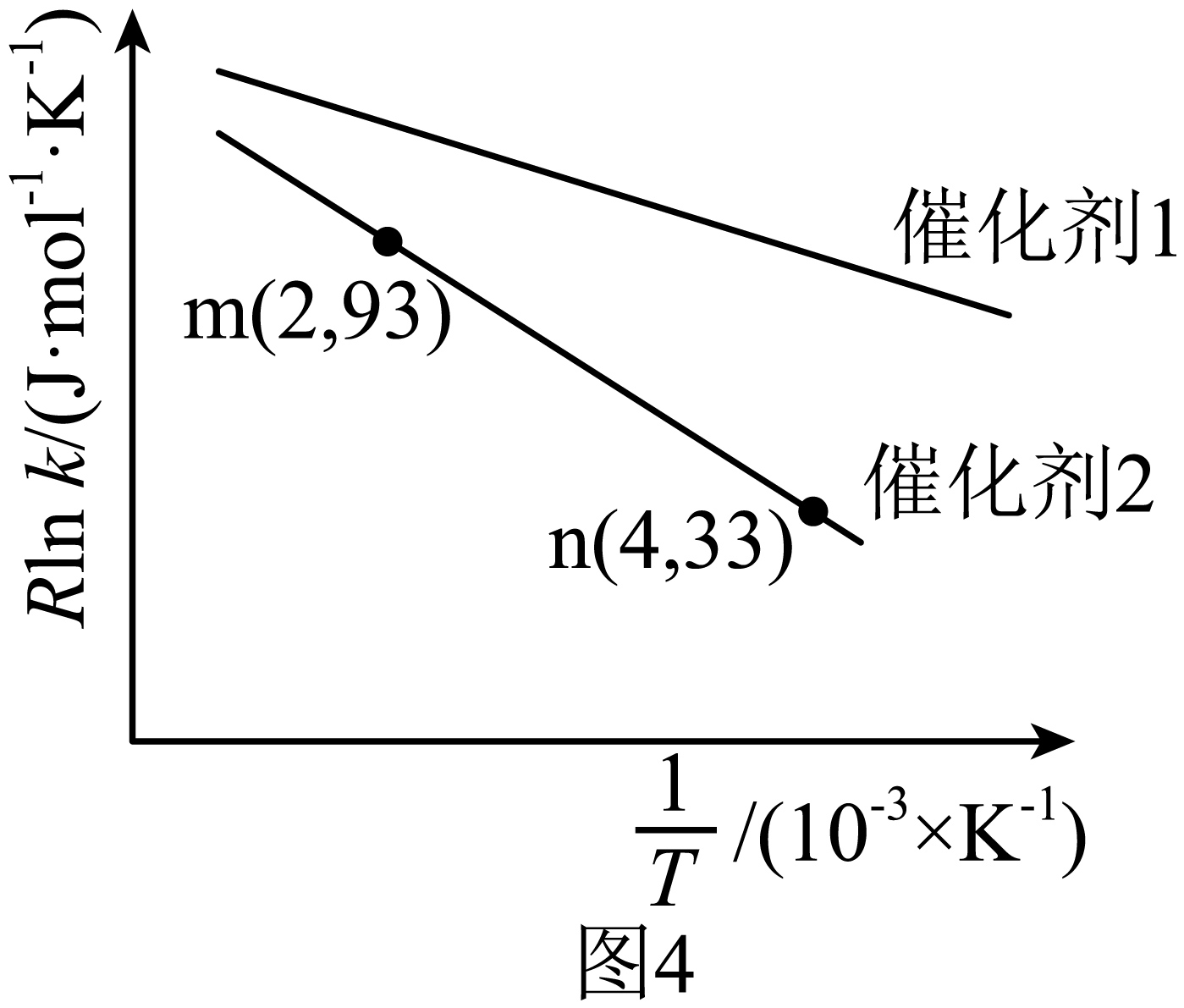
已知$\rm Arrhenius$经验公式为${R{\rm ln}k}=-\dfrac{{{E}_{\text{a}}}}{T}+C ({{{E}}_{\text{a}}}$为活化能，$k$为速率常数，$R$和$C$均为常数$\rm )$。在催化剂$\rm 1$和催化剂$\rm 2$作用下，测得该反应的${R{\rm ln}k}$与$\dfrac{1}{T}$的关系如图$\rm 4$所示。其中催化效率比较高的是                $\rm ($填“催化剂$\rm 1$”或“催化剂$\rm 2$”$\rm )$，在催化剂$\rm 2$的作用下，活化能${{E}_{\text{a}}}=$                $\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$。

催化剂$\\rm 1$ ； $\\rm 30$

根据$\rm Arrhenius$经验公式可知，${R{\rm ln}k}$和$\dfrac{1}{T}$呈反比例关系，从图像上看，直线的斜率的绝对值即为活化能，因此直线的斜率的绝对值越小表示活化能越小，而活化能越小则说明催化剂的效果更好，所以催化效率更高的是催化剂$\rm 1.$将$\text{m}$、$\text{n}$两点的数据代入$\rm Arrhenius$经验公式可得$93\ \text{J}\cdot \text{mo}{{\text{l}}^{-1}}\cdot {{\text{K}}^{-1}}=-{{E}_{\text{a}}}\times {{10}^{3}}\ \text{J}\cdot \text{k}{{\text{J}}^{-1}}\times 2\times {{10}^{-3}}\ {{\text{K}}^{-1}}+C$，$33\ \text{J}\cdot \text{mo}{{\text{l}}^{-1}}\cdot {{\text{K}}^{-1}}=-{{E}_{\text{a}}}\times {{10}^{3}}\ \text{J}\cdot \text{k}{{\text{J}}^{-1}}\times 4\times {{10}^{-3}}\ {{\text{K}}^{-1}}+C$，将两式联立即可得活化能${{E}_{\text{a}}}=30\ \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$。