石油化工路线中，环氧乙烷$\rm (EO)$水合工艺是一种成熟的乙二醇生产方法，环氧乙烷和水反应生成乙二醇，伴随生成二乙二醇$\rm (DEG)$的副反应。

主反应：${\rm EO(aq)+{{H}_{2}}O(l)=EG(aq)}\quad\Delta H\lt 0$

副反应：$\rm EO(aq)+EG(aq)=DEG(aq)$

体系中环氧乙烷初始浓度为$\rm 1.5\ mol\cdot {{L}^{-1}}$，恒温下反应$\rm 30\ min$，环氧乙烷完全转化，产物中$n{\rm (EG)}:n{\rm (DEG)}=10:1$。

①$\rm 0\sim 30\ min$内，${{v}_{总}}\rm (EO)=$                $\rm mol\cdot {{L}^{-1}}\cdot mi{{n}^{-1}}$。

②下列说法正确的是                $\rm ($填序号$\rm )$。

$\rm a$．主反应中，生成物总能量高于反应物总能量

$\rm b$．$\rm 0\sim 30\ min$内，${{v}_{总}}{\rm (EO)}={{v}_{总}}\rm (EG)$

$\rm c$．$\rm 0\sim 30\ min$内，${{v}_{主}}{\rm (EG)}:{{v}_{副}}\rm (DEG)=11:1$

$\rm d$．选择适当催化剂可提高乙二醇的最终产率

$\\rm 0.05\\ mol\\cdot {{L}^{-1}}\\cdot mi{{n}^{-1}}$ ；$\\rm cd$

①$\rm 0\sim 30\ min$内，环氧乙烷完全转化，${{v}_{总}}{\rm (EO)}=\dfrac{\Delta {{c}_{总}}\rm (EO)}{\Delta t}=\rm \dfrac{1.5\ mol\cdot {{L}^{-1}}}{30\ \min }=0.05\ mol\cdot {{L}^{-1}}\cdot mi{{n}^{-1}}$；

②$\rm a$．$\Delta H=生成物总能量-反应物总能量$，主反应中，$\Delta H\lt 0$，则生成物总能量低于反应物总能量，$\rm a$错误；

$\rm b$．由题中信息可知主反应伴随副反应发生，$\rm EG$作为主反应的生成物同时也是副反应的反应物，即$\rm EG$浓度的变化量小于$\rm EO$浓度的变化量，$\rm 0\sim 30\ min$内，$ {{v}_{总}}{\rm (EO)}\gt {{v}_{总}}\rm (EG)$，$\rm b$错误；

$\rm c$．主反应中，${{v}_{主}}{\rm (EG)}={{v}_{主}}\rm (EO)$，副反应${{v}_{副}}{\rm (EG)}={{v}_{副}}\rm (DEG)$，同一反应体系中物质一量变化量之比等于浓度变化量之比，产物中$n{\rm (EG)}:n{\rm (DEG)}=10:1$，即$c{\rm (EG)}:c{\rm (DEG)}=10:1$，${{v}_{总}}{\rm (EG)}={{v}_{主}}{\rm (EG)}-{{v}_{副}}\rm (EG)$，反应时间相同，则${{v}_{总}}{\rm (EG)}:{{v}_{副}}\rm (DEG)=10:1$，$\dfrac{{{v}_{主}}{\rm (EG)}-{{v}_{副}}\rm (EG)}{{{v}_{副}}\rm (DEG)}=10:1$，则${{v}_{主}}{\rm (EG)}:{{v}_{副}}\rm (DEG)=11:1$，$\rm c$正确；

$\rm d$．选择适当催化剂可提高主反应的选择性，可提高 乙二醇的最终产率，$\rm d$正确。

煤化工路线中，利用合成气直接合成乙二醇，原子利用率可达$\rm 100\%$，具有广阔的发展前景。反应如下：${\rm 2CO(g)+3{{H}_{2}}(g)\rightleftharpoons HOC{{H}_{2}}C{{H}_{2}}OH(g)}\quad\Delta H$。按化学计量比进料，固定平衡转化率$\rm \alpha $，探究温度与压强的关系。$\rm \alpha $分别为$\rm 0.4$、$\rm 0.5$和$\rm 0.6$时，温度与压强的关系如图：

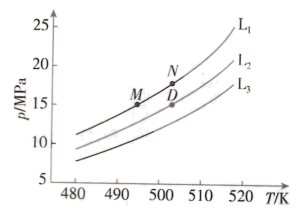
①代表$\rm \alpha=0.6$的曲线为                $\rm ($填“$\rm {{L}_{1}}$”“$\rm {{L}_{2}}$”或“$\rm {{L}_{3}}$”$\rm )$；原因是                。

②$\Delta H$                $\rm 0($填“$\rm \gt $”“$\rm \lt $”或“$\rm =$”$\rm )$。

③已知：反应$ a{\rm A(g)}+b{\rm B(g)}\rightleftharpoons y{\rm Y(g)}+z\rm Z(g)$，${{K}_{x}}=\dfrac{{{x}^{y}}{\rm (Y)}{{x}^{z}}\rm (Z)}{{{x}^{a}}({\rm A}){{x}^{b}}\rm (B)}$，$x$为组分的物质的量分数。$\rm M$、$\rm N$两点对应的体系，${{K}_{x}}\rm (M)$                ${{K}_{x}}\rm (N)($填“$\rm \gt $”“$\rm \lt $”或“$\rm =$”$\rm )$，$\rm D$点对应体系的${{K}_{x}}$的值为                。

④已知：反应$a{\rm A(g)}+b{\rm B(g)}\rightleftharpoons y{\rm Y(g)}+z\rm Z(g)$，${{K}_{\rm p}}=\dfrac{{{p}^{y}}{\rm (Y)}{{p}^{z}}\rm (Z)}{{{p}^{a}}({\rm A}){{p}^{b}}(\rm B)}$，$p$为组分的分压。调整进料比为$n{\rm (CO)}:n{\rm ({{H}_{2}})}=m:3$，系统压强维持${p}_0 \ \rm {MPa}$，使$\rm \alpha({{H}_{2}})=0.75$，此时$ {{K}_{\rm p}}=$                $\rm MP{{a}^{-4}}($用含有$m$和$ {{p}_{0}}$的代数式表示$\rm )$。

$\\rm {{L}_{1}}$； 该反应为气体体积减小的反应，温度相同时，增大压强，平衡正向移动，平衡转化率增大 ；$\\rm \\lt $ ；$\\rm =$； $\\rm 12$； $\\dfrac{1}{{{(\\dfrac{m-1.5}{m}{{p}_{0}}\\ {\\rm MPa})}^{2}}{{(\\dfrac{0.75}{m}{{p}_{0}}\\ \\rm MPa)}^{2}}}$

①${\rm 2CO(g)+3{{H}_{2}}(g)\rightleftharpoons HOC{{H}_{2}}C{{H}_{2}}OH(g)}\quad\Delta H$该反应为气体体积减小的反应，温度相同时，增大压强，平衡正向移动，平衡转化率增大，$p{\rm ({{L}_{1}})}\gt p{\rm ({{L}_{2}})}\gt p{\rm ({{L}_{3}})}$，故$\rm {{L}_{1}}$、$\rm {{L}_{2}}$、$\rm {{L}_{3}}$对应$\rm \alpha$为$\rm 0.6$、$\rm 0.5$、$\rm 0.4$；

②由图可知，压强相同时，温度升高，平衡转化率减小，说明升高温度平衡逆向移动，则正反应为放热反应，$\Delta H\lt 0$；

③$\rm M$、$\rm N$的进料相同，平衡转化率相等，平衡时各组分物质的量分数分别相等，则${{K}_{x}}({\rm M})={{K}_{x}}\rm (N)$；$\rm D$点对应的平衡转化率为$\rm 0.5$，根据题中信息，该反应按化学计量比进料，设起始加入$\rm 2\ mol\ CO$和$\rm 3\ mol\ H_{2}$，列三段式：$\rm \begin{matrix} {} & \rm 2CO(g) & + & \rm 3{{H}_{2}}(g) & \rightleftharpoons & \rm HOC{{H}_{2}}C{{H}_{2}}OH(g) \\ 起始\rm (mol) & 2 & {} & 3 & {} & 0 \\ 转化\rm (mol) & 1 & {} & 1.5 & {} & 0.5 \\ 平衡\rm (mol) & 1 & {} & 1.5 & {} & 0.5 \\ \end{matrix}$，平衡时，$\rm CO$、$\rm {{H}_{2}}$、$\rm HOC{{H}_{2}}C{{H}_{2}}OH$的物质的量分数分别为$\rm \dfrac{1}{3}$、$\dfrac{1}{2}$、$\dfrac{1}{6}$，${{K}_{x}}=\dfrac{\dfrac{1}{6}}{{{(\dfrac{1}{2})}^{3}}{{(\dfrac{1}{3})}^{2}}}=12$；

④设起始加入$m\ \rm mol\ CO$和$\rm 3\ mol\ H_{2}$，此时$\rm \alpha({{H}_{2}})=0.75$，列三段式：$\rm \begin{matrix} {} & \rm 2CO(g) & + & \rm 3{{H}_{2}}(g) & \rightleftharpoons &\rm HOC{{H}_{2}}C{{H}_{2}}OH(g) \\ 起始\rm (mol) & m & {} & 3 & {} & 0 \\ 转化\rm (mol) & 1.5 & {} & 2.25 & {} & 0.75 \\ 平衡\rm (mol) & m-1.5 & {} & 0.75 & {} & 0.75 \\ \end{matrix}$，平衡时，气体总的物质的量为$m\ \rm mol$，$\rm CO$、$\rm {{H}_{2}}$、$\rm HOC{{H}_{2}}C{{H}_{2}}OH$平衡分压分别${p}_0 {\ \rm MPa}$，${{K}_{\rm p}}=\dfrac{\dfrac{0.75}{m}{{p}_{0}}\ \rm MPa}{{{(\dfrac{m-1.5}{m}{{p}_{0}}\ {\rm MPa})}^{2}}{{(\dfrac{0.75}{m}{{p}_{0}}\ {\rm MPa})}^{3}}}=\dfrac{1}{{{(\dfrac{m-1.5}{m}{{p}_{0}}\ {\rm MPa})}^{2}}{{(\dfrac{0.75}{m}{{p}_{0}}\ \rm MPa)}^{2}}}\ \rm MP{{a}^{-4}}$。