已知一定温度下：

$\text{Ca}{{\text{H}}_{2}}(\text{s})+6\text{F}{{\text{e}}_{2}}{{\text{O}}_{3}}(\text{s})=\text{Ca}{{(\text{OH})}_{2}}(\text{s})+4\text{F}{{\text{e}}_{3}}{{\text{O}}_{4}}(\text{s})\quad \Delta {{H}_{1}}=m\text{ kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

$2\text{Ca}{{\text{H}}_{2}}(\text{s})+\text{F}{{\text{e}}_{3}}{{\text{O}}_{4}}(\text{s})=2\text{Ca}{{(\text{OH})}_{2}}(\text{s})+3\text{Fe}(\text{s})\quad \Delta {{H}_{2}}=n\text{ kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

则$3\text{Ca}{{\text{H}}_{2}}(\text{s})+2\text{F}{{\text{e}}_{2}}{{\text{O}}_{3}}(\text{s})=3\text{Ca}{{(\text{OH})}_{2}}(\text{s})+4\text{Fe}(\text{s})$的$\Delta {{H}_{3}}=$                $\;\rm \text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}\rm ($用$m$和$n$表示$\rm )$。

$\\dfrac{m+4n}{3}$

①$\text{Ca}{{\text{H}}_{2}}(\text{s})+6\text{F}{{\text{e}}_{2}}{{\text{O}}_{3}}(\text{s})=\text{Ca}{{(\text{OH})}_{2}}(\text{s})+4\text{F}{{\text{e}}_{3}}{{\text{O}}_{4}}(\text{s})\quad \Delta {{H}_{1}}=m\text{ kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

②$2\text{Ca}{{\text{H}}_{2}}(\text{s})+\text{F}{{\text{e}}_{3}}{{\text{O}}_{4}}(\text{s})=2\text{Ca}{{(\text{OH})}_{2}}(\text{s})+3\text{Fe}(\text{s})\quad \Delta {{H}_{2}}=n\text{ kJ}\cdot \text{mo}{{\text{l}}^{-1}}$

③$3\text{Ca}{{\text{H}}_{2}}(\text{s})+2\text{F}{{\text{e}}_{2}}{{\text{O}}_{3}}(\text{s})=3\text{Ca}{{(\text{OH})}_{2}}(\text{s})+4\text{Fe}(\text{s})\quad \Delta {{H}_{3}}$

$\dfrac{\text{1}}{\text{3}}\rm \times $①$\rm +\dfrac{\text{4}}{\text{3}}\rm \times $②得到反应③，根据盖斯定律可知$\Delta {{H}_{3}} =\dfrac{\text{1}}{\text{3}} \times m\text{ kJ}\cdot \text{mo}{{\text{l}}^{-1}} +\dfrac{\text{4}}{\text{3}} \times n\text{ kJ}\cdot \text{mo}{{\text{l}}^{-1}} =\dfrac{m+4n}{3}\text{ }\text{kJ}\cdot \text{mo}{{\text{l}}^{-1}}$；

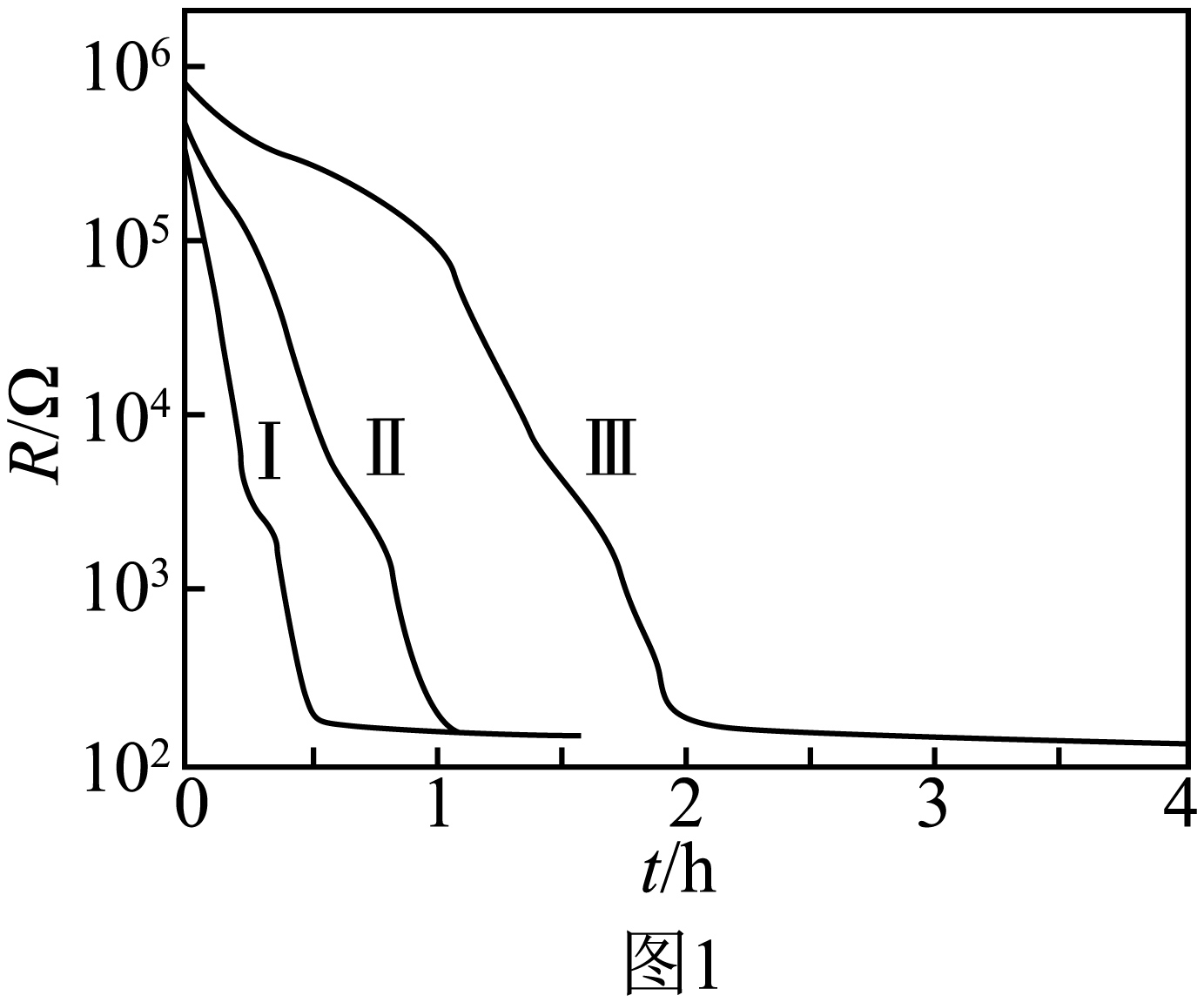
图$1$分别是$260\ {}^\circ \text{C}、280\ {}^\circ \text{C}$和$300\ {}^\circ \text{C}$下$\text{Ca}{{\text{H}}_{\text{2}}}\left( \text{s} \right)$还原$\text{F}{{\text{e}}_{\text{2}}}{{\text{O}}_{\text{3}}}\left( \text{s} \right)$过程中反应体系电阻$R\left( \Omega \right)$随反应时间$t\left( \text{h} \right)$变化的曲线，可用                $\rm ($填标号$\rm )$表示反应的快慢。

$\rm a$．$\dfrac{R}{t}$    $\rm b$．$-\dfrac{\Delta R}{t}$    $\rm c$．$\dfrac{R}{\Delta t}$    $\rm d$．$-\dfrac{\Delta R}{\Delta t}$

$\\rm d$

随着铁的生成，电阻变小，可用单位时间内电阻的变化量来表示反应速率，即$-\dfrac{\Delta R}{\Delta t}$，选$\rm d$；

图$\rm 1$中曲线                $\rm ($填“Ⅰ”“Ⅱ”或“Ⅲ”$\rm )$对应的反应温度最高。

Ⅰ

其它条件相同，温度越高，反应速率越快，曲线Ⅰ电阻变化最快，故曲线Ⅰ对应的反应温度最高；

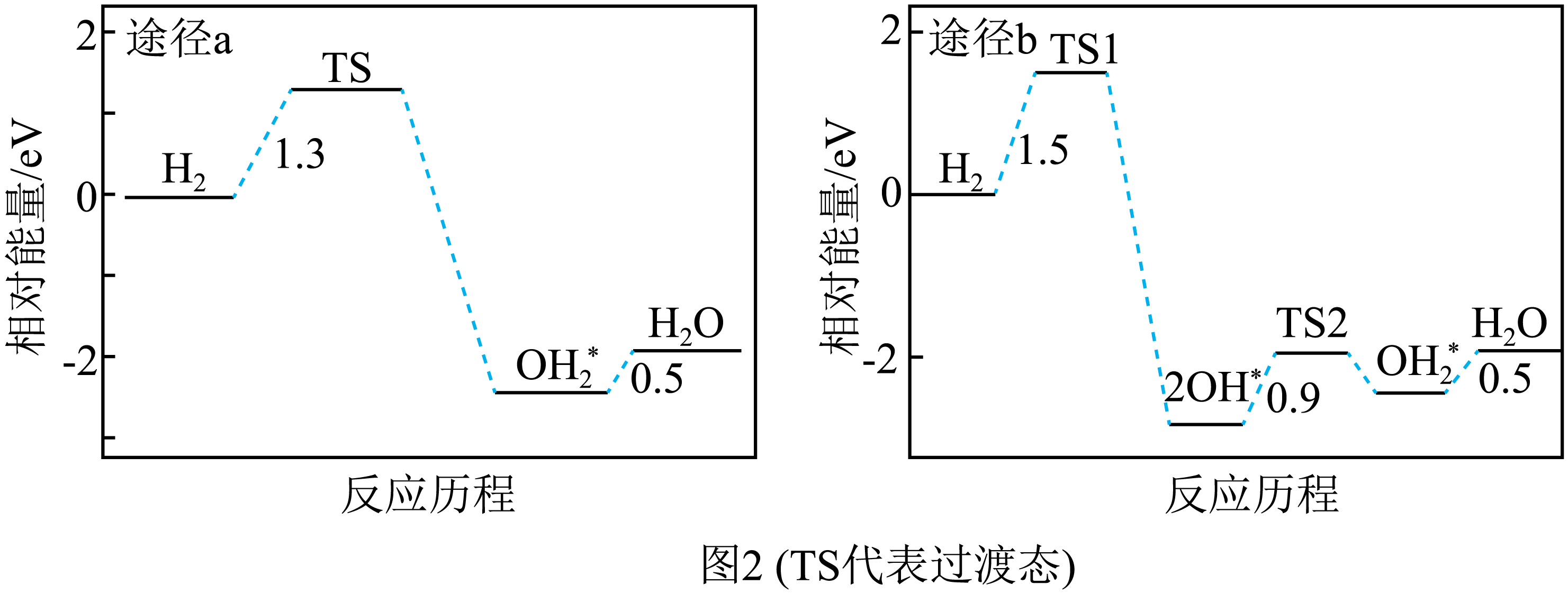
研究发现$\text{Ca}{{\text{H}}_{2}}(\text{s})$对$\text{F}{{\text{e}}_{2}}{{\text{O}}_{3}}(\text{s})$的还原性主要来自于其产生的${{\text{H}}_{2}}$。一般认为${{\text{H}}_{2}}$在$\text{F}{{\text{e}}_{2}}{{\text{O}}_{3}}$表面被氧化成${{\text{H}}_{2}}\text{O}$有两种可能途径，图$\rm 2$是理论计算得到的相对能量变化图，据此推测途径                $\rm ($填“$\rm a$”或“$\rm b$”$\rm )$是主要途径。

$\\rm a$

由图可知途径$\rm a$中能垒为$\rm 1.3$ $\rm eV$，比途径$\rm b$中小，故途径$\rm a$反应速率更快，途径$\rm a$是主要途径；

$\text{Ca}{{\text{H}}_{2}}(\text{s})$产生${{\text{H}}_{2}}$的可能反应：①$\text{Ca}{{\text{H}}_{2}}(\text{s})=\text{Ca}(\text{s})+{{\text{H}}_{2}}(\text{g})$或②$\text{Ca}{{\text{H}}_{2}}(\text{s})+2{{\text{H}}_{2}}\text{O}(\text{g})=\text{Ca}{{(\text{OH})}_{2}}(\text{s})+2{{\text{H}}_{2}}(\text{g})$。将$\text{Ca}{{\text{H}}_{2}}(\text{s})$放在含微量水的${{\text{N}}_{2}}$气流中，在$200\ {}^\circ \text{C}$至$300\ {}^\circ \text{C}$的升温过程中固体质量一直增加，由此可断定${{\text{H}}_{2}}$的来源之一是反应                $\rm ($填“①”或“②”$\rm )$。若要判断另一个反应是否是${{\text{H}}_{2}}$的来源，必须进行的实验是                。

② ； 将$\\rm CaH_{2}(s)$放在不含水的$\\rm N_{2}$气流中加热升温，看固体质量是否在减小

固体质量一直增加，则氢气的来源之一是反应②；若要判断另一个反应是否是$\rm H_{2}$的来源，必须进行的实验是：将$\rm CaH_{2}(s)$放在不含水的$\rm N_{2}$气流中加热升温，看固体质量是否在减小；

已知$3{{\text{H}}_{2}}(\text{g})+\text{F}{{\text{e}}_{2}}{{\text{O}}_{3}}(\text{s})\rightleftharpoons 3{{\text{H}}_{2}}\text{O}(\text{g})+2\text{Fe}(\text{s})$。研究表明，在相同温度下，用$\text{Ca}{{\text{H}}_{2}}(\text{s})$还原$\text{F}{{\text{e}}_{2}}{{\text{O}}_{3}}(\text{s})$比直接用$\mathrm{H}_{2}(\mathrm{g})$还原更有优势，从平衡移动原理角度解释原因：                。

$\\text{Ca}{{\\text{H}}_{2}}(\\text{s})$消耗$\\rm H_{2}O(g)$同时产生$\\rm H_{2}(g)$，$\\rm H_{2}O(g)$的浓度减小，$\\rm H_{2}(g)$的浓度增大均有利于平衡$3{{\\text{H}}_{2}}(\\text{g})+\\text{F}{{\\text{e}}_{2}}{{\\text{O}}_{3}}(\\text{s})\\rightleftharpoons 3{{\\text{H}}_{2}}\\text{O}(\\text{g})+2\\text{Fe}(\\text{s})$正向移动，提高$\\rm Fe$的产率

在相同温度下，用$\text{Ca}{{\text{H}}_{2}}(\text{s})$还原$\text{F}{{\text{e}}_{2}}{{\text{O}}_{3}}(\text{s})$比直接用$\mathrm{H}_{2}(\mathrm{g})$还原更有优势，从平衡移动原理角度解释原因：$\text{Ca}{{\text{H}}_{2}}(\text{s})$消耗$\rm H_{2}O(g)$同时产生$\rm H_{2}(g)$，$\rm H_{2}O(g)$的浓度减小，$\rm H_{2}(g)$的浓度增大均有利于平衡$3{{\text{H}}_{2}}(\text{g})+\text{F}{{\text{e}}_{2}}{{\text{O}}_{3}}(\text{s})\rightleftharpoons 3{{\text{H}}_{2}}\text{O}(\text{g})+2\text{Fe}(\text{s})$正向移动，提高$\rm Fe$的产率。